
【题目】设二次函数f(x)=ax2+bx+c的图象过点(0,1)和(1,4),且对于任意的实数x,不等式f(x)≥4x恒成立.
(1)求函数f(x)的表达式;
(2)设g(x)=kx+1,若F(x)=g(x)﹣f(x),求F(x)在[1,2]上的最小值;
(3)设g(x)=kx+1,若G(x)=![]() 在区间[1,2]上是增函数,求实数k的取值范围.
在区间[1,2]上是增函数,求实数k的取值范围.
【答案】
解:(1)由题意知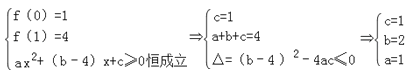
(2)F(x)=g(x)﹣f(x)=﹣x2+(k﹣2)x,x∈[1,2],对称轴x=![]()
当![]() ≤3,即k≤5时,F(x)max=F(2)=2k﹣8
≤3,即k≤5时,F(x)max=F(2)=2k﹣8
当![]()
![]() ,即k>5时,F(x)max=F(1)=k﹣3
,即k>5时,F(x)max=F(1)=k﹣3
综上所述,![]()
(3)G(x)=![]() =
=![]() ,
,
由G(x)在区间[1,2]上是增函数得F(x)=﹣x2+(k﹣2)x在[1,2]上为增函数且恒非负
故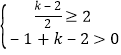
【解析】(1)利用题意,推出混合组,求出a、b、c,即可求函数f(x)的表达式;
(2)化简函数F(x)=g(x)﹣f(x)的表达式,通过对称轴所在位置,讨论即可求F(x)在[1,2]上的最小值
(3)通过![]() 化简表达式,在区间[1,2]上是增函数,转化F(x)=﹣x2+(k﹣2)x在[1,2]上为增函数且恒非负,得到不等式组,即可求实数k的取值范围.
化简表达式,在区间[1,2]上是增函数,转化F(x)=﹣x2+(k﹣2)x在[1,2]上为增函数且恒非负,得到不等式组,即可求实数k的取值范围.
【考点精析】本题主要考查了函数单调性的性质的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=3sin(ωx+φ)(ω>0,﹣![]() <φ<
<φ<![]() )的图象关于直线x=
)的图象关于直线x=![]() 对称,它的周期是π,则以下结论正确的个数( )
对称,它的周期是π,则以下结论正确的个数( )
(1)f(x)的图象过点(0,![]() )
)
(2)f(x)的一个对称中心是(![]() ,0)
,0)
(3)f(x)在[![]() ,
,![]() ]上是减函数
]上是减函数
(4)将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象.
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
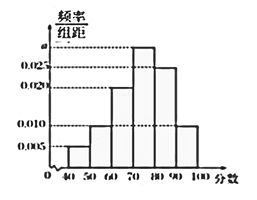
(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
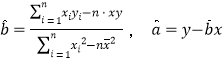 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com