
【题目】设函数f(x)=3sin(ωx+φ)(ω>0,﹣![]() <φ<
<φ<![]() )的图象关于直线x=
)的图象关于直线x=![]() 对称,它的周期是π,则以下结论正确的个数( )
对称,它的周期是π,则以下结论正确的个数( )
(1)f(x)的图象过点(0,![]() )
)
(2)f(x)的一个对称中心是(![]() ,0)
,0)
(3)f(x)在[![]() ,
,![]() ]上是减函数
]上是减函数
(4)将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象.
A.4
B.3
C.2
D.1
【答案】C
【解析】解:∵f(x)=3sin(ωx+φ)(ω>0,﹣![]() <φ<
<φ<![]() )的周期是π,
)的周期是π,
∴ω=2,
又图象关于直线x=![]() 对称,则2×
对称,则2×![]() +φ=kπ+
+φ=kπ+![]() , 即φ=
, 即φ=![]() , k∈Z.
, k∈Z.
∵﹣![]() <φ<
<φ<![]() ,
,
∴取k=1得φ=![]() .
.
∴f(x)=3sin(2x+![]() ).
).
①∵f(0)=3sin![]() =
=![]() .
.
∴f(x)的图象过点(0,![]() )错误;
)错误;
②∵f(![]() )=3sin(2×
)=3sin(2×![]() +
+![]() )=3sinπ=0.
)=3sinπ=0.
∴f(x)的一个对称中心是(![]() ,0)正确;
,0)正确;
③由![]() ,得:
,得:![]() .
.
取k=0,得![]()
∴f(x)在[![]() ,
,![]() ]上是减函数正确;
]上是减函数正确;
④∵φ=![]() >0,
>0,
∴f(x)=3sin(ωx+φ)=3sinω(x+![]() )是把y=3sinωx
)是把y=3sinωx
向左平移![]() 个单位得到,
个单位得到,
则f(x)的图象向右平移![]() 个单位得到函数y=3sinωx的图象.
个单位得到函数y=3sinωx的图象.
∴命题④错误.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
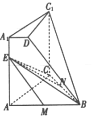
【题目】如图,几何体![]() 由一个正三棱柱截去一个三棱锥而得,
由一个正三棱柱截去一个三棱锥而得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
(1)若![]() 在棱
在棱![]() 上,且
上,且![]() ,证明:
,证明: ![]() 平面
平面![]() ;
;
(2)过![]() 作平面
作平面![]() 的垂线,垂足为
的垂线,垂足为![]() ,确定
,确定![]() 的位置(说明作法及理由),并求线段
的位置(说明作法及理由),并求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是海面上位于东西方向相距5(3+![]() )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20![]() 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?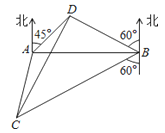
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5个球放入3个盒子,在下列不同条件下,各有多少种投放方法?
①小球不同,盒子不同,盒子不空
②小球不同,盒子不同,盒子可空
③球不同,盒子相同,盒子不空
④小球不同,盒子相同,盒子可空
⑤小球相同,盒子不同,盒子不空
⑥小球相同,盒子不同,盒子可空
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域D,如果存在正实数m,使得对任意x∈D,都有f(x+m)>f(x),则称f(x)为D上的“m型增函数”.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x﹣a|﹣a(a∈R).若f(x)为R上的“20型增函数”,则实数a的取值范围是( )
A.a>0
B.a<5
C.a<10
D.a<20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的环保意识,某市面向全市增招环保知识义务宣传志愿者,从符合条件的志愿者中随机选取![]() 名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第
名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图(局部)如图所示.
,得到的频率分布直方图(局部)如图所示.
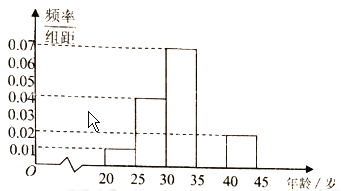
(1)求第![]() 组的频率,并在图中补画直方图;
组的频率,并在图中补画直方图;
(2)从![]() 名志愿者中再选出年龄低于
名志愿者中再选出年龄低于![]() 岁的志愿者
岁的志愿者![]() 名担任主要宣讲人,求这
名担任主要宣讲人,求这![]() 名主要宣讲人的年龄在不同一组的概率.
名主要宣讲人的年龄在不同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx+c的图象过点(0,1)和(1,4),且对于任意的实数x,不等式f(x)≥4x恒成立.
(1)求函数f(x)的表达式;
(2)设g(x)=kx+1,若F(x)=g(x)﹣f(x),求F(x)在[1,2]上的最小值;
(3)设g(x)=kx+1,若G(x)=![]() 在区间[1,2]上是增函数,求实数k的取值范围.
在区间[1,2]上是增函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月份开始采取宏观调控措施,10月份开始房价得到很好的抑制.
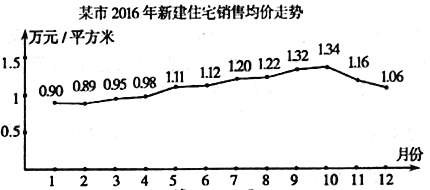
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据及公式: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com