
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,其焦点在圆x2+y2=1上.
,其焦点在圆x2+y2=1上.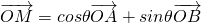 .
.解:(1)依题意,得 c=1.于是,a= ,b=1
,b=1
所以所求椭圆的方程为
(2)(i)设A(x1,y1),B(x2,y2),
则 ①,
①,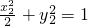 ②.
②.
又设M(x,y),因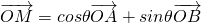 ,故
,故
因M在椭圆上,故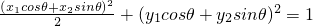 .
.
整理得 .
.
将①②代入上式,并注意cosθsinθ≠0,得  .
.
所以, 为定值
为定值
(ii) ,故y12+y22=1.
,故y12+y22=1.
又 ,故x12+x22=2.
,故x12+x22=2.
所以,OA2+OB2=x12+y12+x22+y22=3
 ,其焦点在圆x2+y2=1上我们可以求出a,b,c的值,进而得到椭圆的方程;
,其焦点在圆x2+y2=1上我们可以求出a,b,c的值,进而得到椭圆的方程;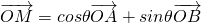 .可得x,y的坐标表达式,进而根据M在椭圆上,可得
.可得x,y的坐标表达式,进而根据M在椭圆上,可得 为定值.
为定值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.| 3 |
| 5 |
| 12 |
| 13 |
| 3 |
| 2 |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com