
����Ŀ��ij��ӰԺ����1000����λ��Ʊ�۲��ֵȴΣ�����ӰԺ�ľ�Ӫ���飬��ÿ��Ʊ�۲�����10Ԫʱ��Ʊ��ȫ�۳�����ÿ��Ʊ�۸���10Ԫʱ��ÿ���1Ԫ������30��Ʊ�����۳���Ϊ�˻�ø��õ����棬���ӰԺ��һ�����ʵ�Ʊ�ۣ�����ϵĻ��������ǣ���Ϊ�˷�����������ˣ�Ʊ�۶�Ϊ1Ԫ�����������ڵ�ӰԺ��һ����Ӱ�ijɱ�����֧��Ϊ5750Ԫ��Ʊ�������������ڳɱ�֧������x��Ԫ����ʾÿ��Ʊ�ۣ���y��Ԫ����ʾ��ӰԺ��ӳһ���ľ����루��ȥ�ɱ�����֧��������룩�ʣ�
��1����y��ʾΪx�ĺ����������䶨����
��2�������ڷ��ϻ���������ǰ���£�Ʊ�۶�Ϊ����ʱ����ӳһ���ľ�������ࣿ
���𰸡�
��1���⣺��ӰԺ����1000����λ����ӰԺ��һ����Ӱ�ijɱ�����֧��Ϊ5750Ԫ��Ʊ�������������ڳɱ�֧����
��x��5.75����Ʊ�����Ϊ6Ԫ��
Ʊ�۲�����10Ԫʱ��
y=1000x��5750����6��x��10����������
Ʊ�۸���10Ԫʱ��
y=x[1000��30��x��10��]��5750
=��30x2+1300x��5750��
�� ![]() ��
��
��ã�5��x��38 ![]() ��
��
��y=��30x2+1300x��5750����10��x��38��������
��2���⣺����y=1000x��5750����6��x��10����������
x=10ʱ��y���Ϊ4250Ԫ��
����y=��30x2+1300x��5750����10��x��38����������
��x=�� ![]() ��21.6ʱ��y���
��21.6ʱ��y���
��Ʊ�۶�Ϊ22Ԫʱ�����������Ϊ8830Ԫ
����������1������x�ķ�Χ���ֱ������������ʽ����2���ֱ�����������������ֵ���Ӷ��ۺϵõ��𰸣�


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�Ķ���A��5��1����AB���ϵ�����CM����ֱ�߷���Ϊ2x��y��5=0��AC���ϵĸ�BH����ֱ�߷���Ϊx��2y��5=0����
��1������C�����ꣻ
��2��ֱ��BC�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��0���գ��У��أ�0��Ϊż�������Һ���y=f��x��ͼ��������ڶԳ����ľ���Ϊ
��0���գ��У��أ�0��Ϊż�������Һ���y=f��x��ͼ��������ڶԳ����ľ���Ϊ ![]() ��
��
��1���� ![]() ��ֵ��
��ֵ��
��2��������y=f��x����ͼ������ƽ�� ![]() ����λ���ٽ��õ���ͼ���ϸ���ĺ������쳤��ԭ����4���������겻�䣬�õ�����y=g��x����ͼ����g��x���ĵ����ݼ����䣮
����λ���ٽ��õ���ͼ���ϸ���ĺ������쳤��ԭ����4���������겻�䣬�õ�����y=g��x����ͼ����g��x���ĵ����ݼ����䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��y=x+b��������C��x2=4y�����ڵ�A�� 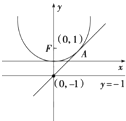
��1����ʵ��b��ֵ��
��2�����Ե�AΪԲ�ģ�����������C�������е�Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��= ![]() ��
��
��1��֤����f��x���Ƕ������ڵ���������
��2����f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ĵȱ�����{an}���㣺a2+a3+a4=28����a3+2��a2 �� a4�ĵȲ�����
��������{an}��ͨ�ʽ��
����bn=anlog2an �� ������{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�һ��һ·���Ľ����У���ʯ�����Ż����ij�����������Ŀ���Ȩ�������ڸõ������������̽�˼��ھ���ȡ���˵�������.����ȫ�濱̽ʱ�ں��Ű�����������þ�λ����ȫ�濱̽.���ڿ�̽һ�ھ��ķ��úܸߣ��������Ƶľ�λ��ԭ�о�λ�غϻ�ӽ��������þɾ��ĵ������ϣ����ش�����¾����Խ�Լ��̽����.��̽�������������±���

(1)��ɢ��ͼ��![]() �žɾ�λ�ô��·ֲ���һ��ֱ�߸���������ǰ5��������ûع��߷���Ϊ
�žɾ�λ�ô��·ֲ���һ��ֱ�߸���������ǰ5��������ûع��߷���Ϊ![]() ����
����![]() ��������
��������![]() ��Ԥ��ֵ��
��Ԥ��ֵ��
(2)������̽�¾�![]() ����ͨ��1��3��5��7�ž��������
����ͨ��1��3��5��7�ž��������![]() ��ֵ(
��ֵ(![]() ��ȷ��0.01)�����(1)��
��ȷ��0.01)�����(1)��![]() ��ֵ֮��(����
��ֵ֮��(����![]() )������10%����ʹ��λ����ӽ������оɾ�
)������10%����ʹ��λ����ӽ������оɾ�![]() ����������λ�ô����жϿɷ�ʹ�þɾ���(�ο���ʽ�ͼ�������
����������λ�ô����жϿɷ�ʹ�þɾ���(�ο���ʽ�ͼ������� ,
,![]() )
)
(3)�����������̽��ȵı�ֵ![]() ������20�Ŀ�̽����Ϊ���ʾ�����ԭ�о���
������20�Ŀ�̽����Ϊ���ʾ�����ԭ�о���![]() �ľ������⿱̽3�ھ�����ǡ��2�������ʾ��ĸ���.
�ľ������⿱̽3�ھ�����ǡ��2�������ʾ��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ҵ繫˾���۲��Ź���200λ����Ա��ÿλ���Ŷ�ÿλ����Ա����1400��Ԫ���������������֪��200λ����Աȥ��������۶������![]() ����λ������Ԫ���ڣ��ֽ���ֳ�5�飬��1�飬��2�飬��3�飬��4�飬��5���Ӧ������ֱ�Ϊ
����λ������Ԫ���ڣ��ֽ���ֳ�5�飬��1�飬��2�飬��3�飬��4�飬��5���Ӧ������ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �����Ƴ�Ƶ�ʷֲ�ֱ��ͼ.
�����Ƴ�Ƶ�ʷֲ�ֱ��ͼ.

��1����![]() ��ֵ�������������������������
��ֵ�������������������������
��2���÷ֲ��������200λ����Ա�г�ȡ����Ϊ25������������5��ֱ�Ӧ��ȡ��������
��3���ִӣ�2�������������������Ա�����ѡȡ2λ�������������������Σ����ô˽�����2λ����Ա��ͬһ��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A={x��R|2x��8=0}��B={x��R|x2��2��m+1��x+m2=0}
��1����m=4����A��B��
��2����A��B=A����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com