考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)证明AC⊥平面BDD1B1,即可证明AC⊥B1D1;
(2)根据平面ABCD∥平面A1B1C1D1,即可证明EF∥平面ABCD;
(3)证明AO⊥平面BEF,即可求三棱锥A-BEF的体积.
解答:
(1)证明:在ABCD-A
1B
1C
1D
1中,连接BD,
因为底面ABCD是正方形
所以AC⊥BD…(1分)
又DD
1⊥平面ABCD,AC?平面ABCD,
所以DD
1⊥AC…(3分)
又BD∩DD
1=D,
所以AC⊥平面BDD
1B
1,
又B
1D
1?平面BDD
1B
1,
所以AC⊥B
1D
1;…(5分)
(2)证明:在ABCD-A
1B
1C
1D
1中,平面ABCD∥平面A
1B
1C
1D
1,
因为EF?平面A
1B
1C
1D
1,
所以EF∥平面ABCD;…(10分)
(3)解:设AC与BD交于点O,由(1)可知AO⊥平面BDD
1B
1,
即AO⊥平面BEF
所以AO是三棱锥A-BEF的高,且AO=
AC=
…(12分)
所以V
A-BEF=
××××2=
…(14分)
点评:本题考查线面垂直的判定与性质,考查线面平行,考查锥体体积的计算,考查学生分析解决问题的能力,属于中档题.

 如图,长方体ABCD-A1B1C1D1的底面是正方形,AB=1,AA1=2,线段B1D1上有两个点E,F.
如图,长方体ABCD-A1B1C1D1的底面是正方形,AB=1,AA1=2,线段B1D1上有两个点E,F.

 能力评价系列答案
能力评价系列答案 某学校进行自主实验教育改革,选取甲、乙两个班做对比实验,甲班采用传统教育方式,乙班采用学生自主学习,学生可以针对自己薄弱学科进行练习,教师不做过多干预,两班人数相同,为了检验教学效果,现从两班各随机抽取20名学生的期末总成绩,得到以下的茎叶图:
某学校进行自主实验教育改革,选取甲、乙两个班做对比实验,甲班采用传统教育方式,乙班采用学生自主学习,学生可以针对自己薄弱学科进行练习,教师不做过多干预,两班人数相同,为了检验教学效果,现从两班各随机抽取20名学生的期末总成绩,得到以下的茎叶图: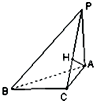 如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.
如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值. 如图在△ABC的长边AB上取AN=AC,BM=BC,点I为三角形ABC的内心 求证:
如图在△ABC的长边AB上取AN=AC,BM=BC,点I为三角形ABC的内心 求证: