
【题目】已知等比数列![]() 满足:
满足:![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
【答案】(1)an=![]() ·3n-1,或an=-5·(-1)n-1.
·3n-1,或an=-5·(-1)n-1.
(2)不存在正整数m,使得![]() ≥1成立.
≥1成立.
【解析】
试题(1)将已知条件转化为等比数列的首项和公比表示,转化为关于![]() 的方程组,通过解方程组得到
的方程组,通过解方程组得到![]() 的值,从而得到数列的通项公式;(2)将数列
的值,从而得到数列的通项公式;(2)将数列![]() 的通项公式代入
的通项公式代入![]() 求和,分情况判断对应的不等式是否成立
求和,分情况判断对应的不等式是否成立
试题解析:(1)设等比数列{an}的公比为q,
则由已知可得
解得![]() 或
或![]()
故an=![]() ·3n-1,或an=-5·(-1)n-1.
·3n-1,或an=-5·(-1)n-1.
(2)若an=![]() ·3n-1,则
·3n-1,则![]() =
=![]() ·(
·(![]() )n-1.
)n-1.
故{![]() }是首项为
}是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
从而 .
.
若an=-5·(-1)n-1,则![]() =-
=-![]() (-1)n-1.
(-1)n-1.
故{![]() }是首项为-
}是首项为-![]() ,公比为-1的等比数列.
,公比为-1的等比数列.
从而![]() =
= 故
故![]() <1.
<1.
综上,对任何正整数m,总有![]() <1.
<1.
故不存在正整数m,使得![]() ≥1成立.
≥1成立.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】光线从![]() 点射出,到
点射出,到![]() 轴上的
轴上的![]() 点后,被
点后,被![]() 轴反射到
轴反射到![]() 轴上的
轴上的![]() 点,又被
点,又被![]() 轴反射,这时反射线恰好过点
轴反射,这时反射线恰好过点![]() .
.
(1)求![]() 所在直线的方程;
所在直线的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() ,
,![]() 轴分别交于
轴分别交于![]() 、
、![]() ,过
,过![]() 、
、![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.经过任意三点有且只有一个平面.
B.过点![]() 有且仅有一条直线与异面直线
有且仅有一条直线与异面直线![]() 垂直.
垂直.
C.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行.
D.面![]() 与平面
与平面![]() 相交,则公共点个数为有限个.
相交,则公共点个数为有限个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门从某超市销售的甲、乙两种食用油中分别随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图:
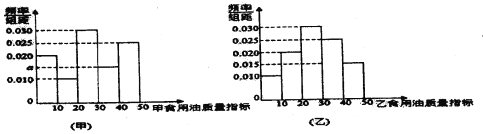
(I)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,试比较
,试比较![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)佑计在甲、乙两种食用油中各随机抽取1桶,恰有一个桶的质量指标大于20,且另—个桶的质量指标不大于20的概率;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]() :
:
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com