
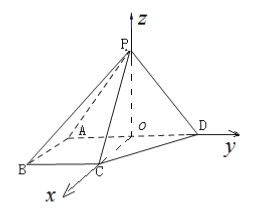
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
, ![]()
![]() .
.
(1)证明: ![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,由正三角形性质得
,由正三角形性质得![]() ,由矩形的性质得
,由矩形的性质得![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ,从而可得结论;(2)
,从而可得结论;(2)![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用空间向量夹角的余弦公式可得结果.
的法向量,利用空间向量夹角的余弦公式可得结果.
试题解析:(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() .底面
.底面![]() 中,可得四边形
中,可得四边形![]() 为矩形,
为矩形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .又
.又![]() ,所以
,所以![]() .
.
(2)由面![]() 面
面![]() 知,
知, ![]() 平面
平面![]() ,
, ![]() 两两垂直,直线
两两垂直,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即
,即![]() ,由
,由![]() ,知
,知![]() ,得
,得![]() .分别以
.分别以![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,则
,则![]()
![]()
![]() ,
, ![]()
![]() , 设平面
, 设平面![]() 的法向量为
的法向量为![]() .
.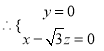 ,则
,则![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
, 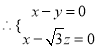 ,则
,则![]() ,
, 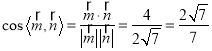 ,
,![]() 由图可知二面角
由图可知二面角![]() 的余弦值
的余弦值![]() .
.
【方法点晴】本题主要考查线面垂直的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)求函数f(x)的单调区间;
(2)设a>0,求函数f(x)在[2a,4a]上的最小值;
(3)某同学发现:总存在正实数a、b(a<b),使ab=ba , 试问:他的判断是否正确?若不正确,请说明理由;若正确,请直接写出a的取值范围(不需要解答过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数f(x)的图象经过点(0, ![]() ),且f′(x)=﹣x﹣1,则不等式f(10x)>0的解集为( )
),且f′(x)=﹣x﹣1,则不等式f(10x)>0的解集为( )
A.(﹣3,1)
B.(﹣lg3,0)
C.( ![]() ,1)
,1)
D.(﹣∞,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于
为大于![]() 的常数),现随机抽取
的常数),现随机抽取![]() 件合格产品,测得数据如下:
件合格产品,测得数据如下:
尺寸 |
|
|
|
|
|
|
质量 |
|
|
|
|
|
|
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的
内时为优等品,现从抽取的![]() 件合格产品中再任选
件合格产品中再任选![]() 件,记
件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一条公路上,每隔100km有个仓库(如图),共有5个仓库.一号仓库存有10t货物,二号仓库存20t,五号仓库存40t,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输1km需要0.5元运输费,那么要多少才行? ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且在区间(0,+∞)上是单调递增,若 ![]() ,△ABC的内角满足f(cosA)<0,则A的取值范围是( )
,△ABC的内角满足f(cosA)<0,则A的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,π)
,π)
C.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
D.( ![]() ,
, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com