
【题目】已知平行四边形![]() 中
中![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,三角形
,三角形![]() 为等边三角形,
为等边三角形,![]() .
.
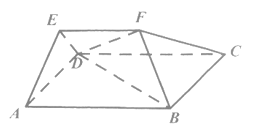
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]()
①求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
②求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)①![]() ;②
;②![]() .
.
【解析】
(Ⅰ)先证明![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴建立空间直角坐标系,利用向量的数量积为零可得
轴建立空间直角坐标系,利用向量的数量积为零可得![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,再由面面垂直的判定定理可得结果;(Ⅱ)设
,再由面面垂直的判定定理可得结果;(Ⅱ)设![]() ,利用
,利用![]() ,求得
,求得![]() ,①求出
,①求出![]() ,
,![]() 的坐标,利用空间向量夹角余弦公式可得结果;②利用向量垂直数量积为零列方程,分别求出平面
的坐标,利用空间向量夹角余弦公式可得结果;②利用向量垂直数量积为零列方程,分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,由空间向量夹角余弦公式求得二面角的余弦值,进而可得结果.
的法向量,由空间向量夹角余弦公式求得二面角的余弦值,进而可得结果.
(Ⅰ)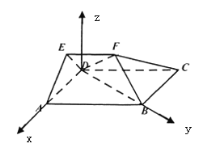
平行四边形![]() 中
中
∵![]() ,
,![]() ,
,
由余弦定理可得![]() ,
,
由勾股定理可得![]() ,
,
如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]()
∴![]() ,
,,
![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(Ⅱ)∵![]() ,∴设
,∴设![]()
∴![]() ,
,![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() .
.
①![]() ,
,![]()
∴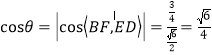
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
②设![]() 为平面
为平面![]() 的法向量,则
的法向量,则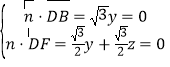
可得![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则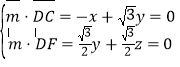
可得![]() ,
,
∴![]() ,
,![]()
∴二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】 下列结论错误的是
A. 命题:“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 命题:“![]() ,
, ![]() ”的否定是“
”的否定是“![]() ,
, ![]() ”
”
D. 若“![]() ”为假命题,则
”为假命题,则![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年入夏以来,我市天气反复,降雨频繁.在下图中统计了上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是()
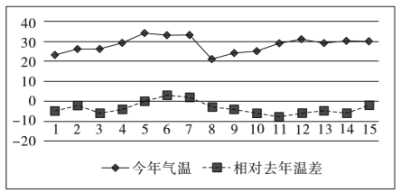
A.今年每天气温都比去年气温高B.今年的气温的平均值比去年低
C.去年8-11号气温持续上升D.今年8号气温最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研学旅行是研究性学习和旅行体验相结合的校外教育活动,继承和发展了我国传统游学、“读万卷书,行万里路”的教育理念和人文精神,成为素质教育的新内容和新方式,提升中小学生的自理能力、创新精神和实战能力,是综合实战育人的有效途径,为了了解某校高二年级600名学生在一次研学旅行活动中的武术表演情况,研究人员在该校高二学生中随机抽取了10名学生的武术表演成绩进行统计,统计结果如图所示(满分100分),已知这10名学生或武术表演的平均成绩为85分.
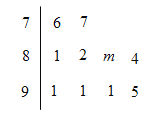
(1)求m的值;
(2)为了研究高二男、女生的武术表演情况,现对该校高二所有学生的武术表演成绩进行分类统计,得到的数据如下表所示:
男生 | 女生 | 合计 | |
武术表演成绩超过80分 | 150 | ||
武术表演成绩不超过80分 | 100 | ||
合计 |
已知随机抽取这600名学生中的一名学生,抽到武术表演成绩超过80分的学生概率是![]() ,根据已知条件完成上面
,根据已知条件完成上面![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为武术表演成绩超过80分与性别具有相关性.
的把握认为武术表演成绩超过80分与性别具有相关性.
参考公式: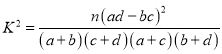 ,其中
,其中![]() .
.
临界值表:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员射击一次所得环数![]() 的分布如下:
的分布如下:
|
| 7 | 8 | 9 | 10 |
| 0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率.
(Ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有4个小球,小球上分别写有0,1,2,3的数字,小球除数字外其他完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.抽奖活动的奖励规则是:①若取出的两个小球上数字之积大于4,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间上![]() ,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左顶点为
的左顶点为![]() ,右顶点为
,右顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,且以线段
,且以线段![]() 为直径的圆被直线
为直径的圆被直线![]() 所截得的弦长为
所截得的弦长为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,且点
,且点![]() 在第一象限,点
在第一象限,点![]() 关于
关于![]() 轴对称点为点
轴对称点为点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若直线
,若直线![]() 斜率大于
斜率大于![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com