
【题目】某运动员射击一次所得环数![]() 的分布如下:
的分布如下:
|
| 7 | 8 | 9 | 10 |
| 0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率.
(Ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
【答案】(I) 0.04
(II)

(III) 9.07
【解析】
本试题主要考查了独立事件概率的乘法公式好分布列的求解,以及期望公式的的综合运用。
(1)中,利用两次都命中事件同时发生的概率乘法公式得到
(2)中,因为由题意可知ξ可能取值为7、8、9、10,那么分别得到各个取值的概率值,得到分布列。
(3)利用期望公式求解期望值。
解:(I)由题意知运动员两次射击是相互独立的,根据相互独立事件同时发生的概率得到,该运动员两次都命中7环的概率为P=0.2×0.2=0.04
(II)ξ可能取值为7、8、9、10
P(ξ=7)=0.04 P(ξ=8)=2×0.2×0.3+0.32=0.21
P(ξ=9)=2×0.2×0.3+2×0.3×0.3+0.32=0.39
P(ξ=10)=2×0.2×0.2+2×0.3×0.2+2×0.3×0.2+0.22=0.36
∴ξ的分布列为

∴ξ的数学期望为Eξ=7×0.04+8×0.21+9×0.39+10×0.36=9.07


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() ,其前
,其前![]() 项和为
项和为![]() ,且
,且![]() 为等比数列.
为等比数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .设
.设![]() 是整数,问是否存在正整数
是整数,问是否存在正整数![]() ,使等式
,使等式![]() 成立?若存在,求出
成立?若存在,求出![]() 和相应的
和相应的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金(奖金额![]() 元)、专业二等奖学金(奖金额
元)、专业二等奖学金(奖金额![]() 元)及专业三等奖学金(奖金额
元)及专业三等奖学金(奖金额![]() 元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校
元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校![]() 年
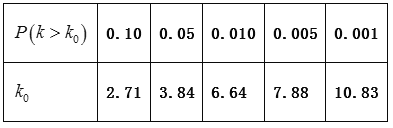
年![]() 名学生周课外平均学习时间频率分布直方图,图(2)是这
名学生周课外平均学习时间频率分布直方图,图(2)是这![]() 名学生在
名学生在![]() 年周课外平均学习时间段获得专业奖学金的频率柱状图.
年周课外平均学习时间段获得专业奖学金的频率柱状图.
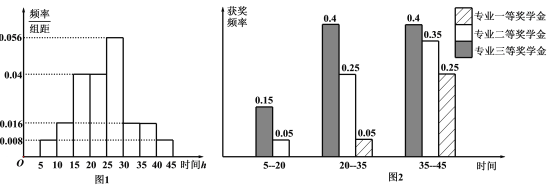
(Ⅰ)求这![]() 名学生中获得专业三等奖学金的人数;
名学生中获得专业三等奖学金的人数;
(Ⅱ)若周课外平均学习时间超过![]() 小时称为“努力型”学生,否则称为“非努力型”学生,列
小时称为“努力型”学生,否则称为“非努力型”学生,列![]() 联表并判断是否有
联表并判断是否有![]() 的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
(Ⅲ)若以频率作为概率,从该校任选一名学生,记该学生![]() 年获得的专业奖学金额为随机变量
年获得的专业奖学金额为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.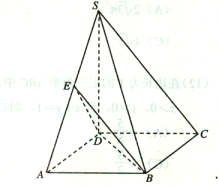
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海轮每小时使用的燃料费与它的航行速度的立方成正比,已知某海轮的最大航速为![]() 海里/小时, 当速度为
海里/小时, 当速度为![]() 海里/小时时,它的燃料费是每小时
海里/小时时,它的燃料费是每小时![]() 元,其余费用(无论速度如何)都是每小时
元,其余费用(无论速度如何)都是每小时![]() 元.如果甲乙两地相距
元.如果甲乙两地相距![]() 海里,则要使该海轮从甲地航行到乙地的总费用最低,它的航速应为( )
海里,则要使该海轮从甲地航行到乙地的总费用最低,它的航速应为( )
A.![]() 海里/小时B.
海里/小时B.![]() 海里/小时
海里/小时
C.![]() 海里/小时D.
海里/小时D.![]() 海里/小时
海里/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com