
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.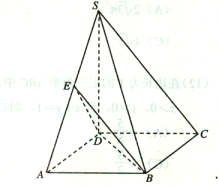
【答案】(1)详见解析(2)![]() .
.
【解析】
解:
(Ⅰ)∵SD⊥平面ABCD,∴平面SAD⊥平面ABCD,
∵AB⊥AD,∴AB⊥平面SAD,∴DE⊥AB.
∵SD=AD,E是SA的中点,∴DE⊥SA,
∵AB∩SA=A,∴DE⊥平面SAB
∴平面BED⊥平面SAB. …4分
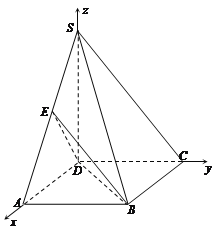
(Ⅱ)建立如图所示的坐标系D—xyz,不妨设AD=2,则
D(0,0,0),A(2,0,0),B(2,![]() ,0),
,0),
C(0,![]() ,0),S(0,0,2),E(1,0,1).
,0),S(0,0,2),E(1,0,1).
![]() =(2,
=(2,![]() ,0),
,0),![]() =(1,0,1),
=(1,0,1),![]() =(2,0,0),
=(2,0,0),![]() =(0,-
=(0,-![]() ,2).
,2).
设m=(x1,y1,z1)是面BED的一个法向量,则 因此可取m=(-1,
因此可取m=(-1,![]() ,1). …8分
,1). …8分
设n=(x2,y2,z2)是面SBC的一个法向量,则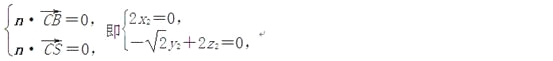 因此可取n=(0,
因此可取n=(0,![]() ,1). …10分
,1). …10分
 故平面BED与平面SBC所成锐二面角的大小为30°.…12分
故平面BED与平面SBC所成锐二面角的大小为30°.…12分


科目:高中数学 来源: 题型:
【题目】某运动员射击一次所得环数![]() 的分布如下:
的分布如下:
|
| 7 | 8 | 9 | 10 |
| 0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率.
(Ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
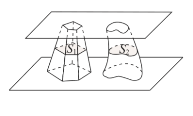
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的
A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文化创意公司开发出一种玩具(单位:套)进行生产和销售.根据以往经验,每月生产x套玩具的成本p由两部分费用(单位:元)构成:![]() .固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本
.固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本![]() .
.
(1)问:该公司每月生产玩具多少套时,可使得平均每套所需成本费用最少?此时每套玩具的成本费用是多少?
(2)假设每月生产出的玩具能全部售出,但随着x的增大,生产所需的直接总成本在急剧增加,因此售价也需随着x的增大而适当增加.设每套玩具的售价为q元,![]() (
(![]() ).若当产量为15000套时利润最大,此时每套售价为300元,试求
).若当产量为15000套时利润最大,此时每套售价为300元,试求![]() 、b的值.(利润=销售收入-成本费用)
、b的值.(利润=销售收入-成本费用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com