
【题目】某文化创意公司开发出一种玩具(单位:套)进行生产和销售.根据以往经验,每月生产x套玩具的成本p由两部分费用(单位:元)构成:![]() .固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本
.固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本![]() .
.
(1)问:该公司每月生产玩具多少套时,可使得平均每套所需成本费用最少?此时每套玩具的成本费用是多少?
(2)假设每月生产出的玩具能全部售出,但随着x的增大,生产所需的直接总成本在急剧增加,因此售价也需随着x的增大而适当增加.设每套玩具的售价为q元,![]() (
(![]() ).若当产量为15000套时利润最大,此时每套售价为300元,试求
).若当产量为15000套时利润最大,此时每套售价为300元,试求![]() 、b的值.(利润=销售收入-成本费用)
、b的值.(利润=销售收入-成本费用)
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金(奖金额![]() 元)、专业二等奖学金(奖金额
元)、专业二等奖学金(奖金额![]() 元)及专业三等奖学金(奖金额
元)及专业三等奖学金(奖金额![]() 元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校
元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校![]() 年
年![]() 名学生周课外平均学习时间频率分布直方图,图(2)是这
名学生周课外平均学习时间频率分布直方图,图(2)是这![]() 名学生在
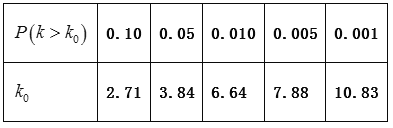
名学生在![]() 年周课外平均学习时间段获得专业奖学金的频率柱状图.
年周课外平均学习时间段获得专业奖学金的频率柱状图.
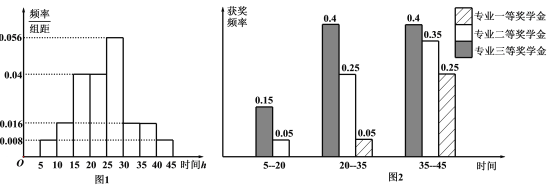
(Ⅰ)求这![]() 名学生中获得专业三等奖学金的人数;
名学生中获得专业三等奖学金的人数;
(Ⅱ)若周课外平均学习时间超过![]() 小时称为“努力型”学生,否则称为“非努力型”学生,列
小时称为“努力型”学生,否则称为“非努力型”学生,列![]() 联表并判断是否有
联表并判断是否有![]() 的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
(Ⅲ)若以频率作为概率,从该校任选一名学生,记该学生![]() 年获得的专业奖学金额为随机变量
年获得的专业奖学金额为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
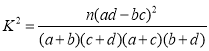
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.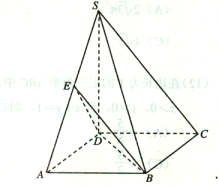
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,D,E,F分别是B1C1,AB,AA1的中点.
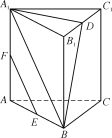
(1) 求证:EF∥平面A1BD;
(2) 若A1B1=A1C1,求证:平面A1BD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产![]() (千部)手机,需另投入成本
(千部)手机,需另投入成本![]() 万元,且
万元,且  ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(![]() )求出2020年的利润
)求出2020年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
![]() 2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,![]() .
.
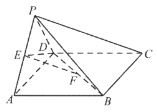
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海轮每小时使用的燃料费与它的航行速度的立方成正比,已知某海轮的最大航速为![]() 海里/小时, 当速度为
海里/小时, 当速度为![]() 海里/小时时,它的燃料费是每小时
海里/小时时,它的燃料费是每小时![]() 元,其余费用(无论速度如何)都是每小时
元,其余费用(无论速度如何)都是每小时![]() 元.如果甲乙两地相距
元.如果甲乙两地相距![]() 海里,则要使该海轮从甲地航行到乙地的总费用最低,它的航速应为( )
海里,则要使该海轮从甲地航行到乙地的总费用最低,它的航速应为( )
A.![]() 海里/小时B.
海里/小时B.![]() 海里/小时
海里/小时
C.![]() 海里/小时D.
海里/小时D.![]() 海里/小时
海里/小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知在一个极坐标系中点![]() 的极坐标为
的极坐标为![]() .
.
(1)求出以![]() 为圆心,半径长为2的圆的极坐标方程(写出解题过程)并画出图形.
为圆心,半径长为2的圆的极坐标方程(写出解题过程)并画出图形.
(2)在直角坐标系中,以圆![]() 所在极坐标系的极点为原点,极轴为
所在极坐标系的极点为原点,极轴为![]() 轴的正半轴建立直角坐标系,点
轴的正半轴建立直角坐标系,点![]() 是圆
是圆![]() 上任意一点,
上任意一点, ![]() ,
, ![]() 是线段
是线段![]() 的中点,当点
的中点,当点![]() 在圆
在圆![]() 上运动时,求点
上运动时,求点![]() 的轨迹的普通方程.
的轨迹的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com