
【题目】设函数f(x)=![]() .
.
(1)当m=4时,求函数f(x)的定义域M;
(2)当a,b∈![]() RM时,证明:2|a+b|<|4+ab|.
RM时,证明:2|a+b|<|4+ab|.
【答案】(1)M={x|x≤﹣2或x≥2};(2)见解析.
【解析】
试题(1)由题意和二次根式的被开方数非负,可得|x+1|+|x﹣1|≥4,运用绝对值的意义和对x讨论,解不等式即可得到所求定义域;
(2)可得﹣2<a,b<2,要证2|a+b|<|4+ab|,可证4(a+b)2<(4+ab)2,作差4(a+b)2﹣(4+ab)2,运用平方差和因式分解,即可得证.
试题解析:
(1)解:当m=4时,由|x+1|+|x﹣1|≥4,
等价于 ![]() 或
或 ![]() 或
或 ![]() ,
,
解得x≤﹣2或x≥2或x∈.
则不等式的解集为M={x|x≤﹣2或x≥2}
(2)解:证明:当a,b∈CRM时,即﹣2<a,b<2,
所以4(a+b)2﹣(4+ab)2=4(a2+2ab+b2)﹣(16+8ab+a2b2)
=4a2+4b2﹣16﹣a2b2=(a2﹣4)(4﹣b2)<0,所以4(a+b)2<(4+ab)2,
即2|a+b|<|4+ab|.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】某文化创意公司开发出一种玩具(单位:套)进行生产和销售.根据以往经验,每月生产x套玩具的成本p由两部分费用(单位:元)构成:![]() .固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本
.固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本![]() .
.
(1)问:该公司每月生产玩具多少套时,可使得平均每套所需成本费用最少?此时每套玩具的成本费用是多少?
(2)假设每月生产出的玩具能全部售出,但随着x的增大,生产所需的直接总成本在急剧增加,因此售价也需随着x的增大而适当增加.设每套玩具的售价为q元,![]() (
(![]() ).若当产量为15000套时利润最大,此时每套售价为300元,试求
).若当产量为15000套时利润最大,此时每套售价为300元,试求![]() 、b的值.(利润=销售收入-成本费用)
、b的值.(利润=销售收入-成本费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,且过点
,且过点![]() .
.
(![]() )求椭圆
)求椭圆![]() 的标准方程.
的标准方程.
(![]() )
)![]() 、
、![]() 、
、![]() 、
、![]() 是椭圆
是椭圆![]() 上的四个不同的点,两条都不和
上的四个不同的点,两条都不和![]() 轴垂直的直线
轴垂直的直线![]() 和
和![]() 分别过点
分别过点![]() ,
, ![]() ,且这条直线互相垂直,求证:
,且这条直线互相垂直,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
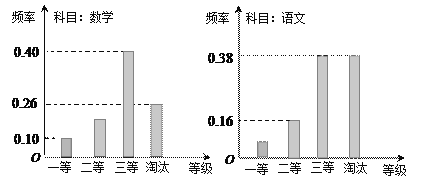

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com