
【题目】如图,在直三棱柱ABCA1B1C1中,D,E,F分别是B1C1,AB,AA1的中点.
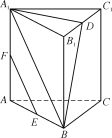
(1) 求证:EF∥平面A1BD;
(2) 若A1B1=A1C1,求证:平面A1BD⊥平面BB1C1C.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先证出EF∥A1B,利用线面平行的判定定理即可证出.
(2)证出BB1⊥A1D,A1D⊥B1C1,利用面面垂直的判定定理即可证出.
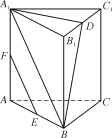
因为E,F分别是AB,AA1的中点,所以EF∥A1B.
因为EF平面A1BD,A1B平面A1BD,所以EF∥平面A1BD.
(2)在直三棱柱ABCA1B1C1中,BB1⊥平面A1B1C1,因为A1D平面A1B1C1,所以BB1⊥A1D.
因为A1B1=A1C1,且D是B1C1的中点,所以A1D⊥B1C1.
因为BB1![]() B1C1=B1,B1C1,BB1平面BB1C1C,所以A1D⊥平面BB1C1C.
B1C1=B1,B1C1,BB1平面BB1C1C,所以A1D⊥平面BB1C1C.
因为A1D平面A1BD,所以平面A1BD⊥平面BB1C1C.


科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.

(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)具有较强的相关性,且两者之间有如下对应数据:
(单位:万元)具有较强的相关性,且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中的线性回归方程,当广告费支出为10万元时,预测销售额是多少?
参考数据: ![]() ,
,![]() ,
,![]() 。
。
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.

(Ⅰ) 求证:OC⊥PD;
(II)若PD与平面PAB所成的角为30°,求二面角D-PC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com