
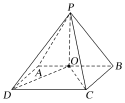
【题目】如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.

(Ⅰ) 求证:OC⊥PD;
(II)若PD与平面PAB所成的角为30°,求二面角D-PC-B的余弦值.
【答案】(I)详见解析(II)![]()
【解析】
(Ⅰ)连结OP,推导出OP⊥AB,从而OP⊥平面ABCD,由OP⊥OD,OP⊥OC,得OD⊥OC,再由OP⊥OC,能证明OC⊥PD.
(Ⅱ)取CD的中点E,以O为原点,OE,OB,OP所在的直线分别为x,y,z轴建立空间直角坐标系O-xyz.求出平面DPC与平面BPC的法向量,由此能求出二面角D﹣PC﹣B的余弦值.
(I)证明 如图,连接OP.
∵PA=PB,O为AB的中点,
∴OP⊥AB.
∵侧面PAB⊥底面ABCD,
∴OP⊥平面ABCD,
∴OP⊥OD,OP⊥OC.
∵OD⊥PC,∴OD⊥平面OPC,
∴OD⊥OC,
又OP⊥OC,OP∩OD=O,
∴OC⊥平面OPD,
∴OC⊥PD.
(II)解:法一 取CD的中点E,以O为原点,OE,OB,OP所在的直线分别为x,y,z轴建立空间直角坐标系O-xyz.在矩形ABCD中,由(1)得OD⊥OC,∴AB=2AD,不妨设AD=1,则AB=2.
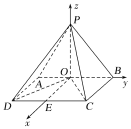
∵侧面PAB⊥底面ABCD,底面ABCD为矩形,
∴DA⊥平面PAB,CB⊥平面PAB,△DPA≌△CPB,
∴∠DPA为直线PD与平面PAB所成的角,
∴∠DPA=30°,∠CPB=30°,PA=PB=![]() ,
,
∴B(0,1,0),C(1,1,0),D(1,-1,0),P(0,0,![]() ),从而
),从而![]() =(1,1,-
=(1,1,-![]() ),
),![]() =(0,-2,0).
=(0,-2,0).
设平面PCD的法向量为n1=(x1,y1,z1),
由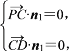 得
得![]() 可取n1=(
可取n1=(![]() ,0,1).
,0,1).
同理,可取平面PCB的一个法向量为n2=(0,-![]() ,-1).
,-1).
于是cos〈n1,n2〉=![]() =-
=-![]() ,
,
∴二面角D-PC-B的余弦值为-![]() .
.
法二 在矩形ABCD中,由(1)得OD⊥OC,∴AB=2AD,不妨设AD=1,则AB=2.
∵侧面PAB⊥底面ABCD,底面ABCD为矩形,
∴DA⊥平面PAB,CB⊥平面PAB,△DPA≌△CPB,
∴∠DPA为直线PD与平面PAB所成的角,
∴∠DPA=30°,∠CPB=30°,PA=PB=![]() ,
,
∴DP=CP=2,
∴△PDC为等边三角形.
设PC的中点为M,连接DM,则DM⊥PC.
在Rt△CBP中,过M作NM⊥PC,交PB于点N,连接ND,则∠DMN为二面角D-PC-B的一个平面角.
由于∠CPB=30°,PM=1,故在Rt△PMN中,MN=![]() ,PN=
,PN=![]() .
.
∵cos∠APB=![]() =
=![]() ,
,
∴AN2=![]()
![]() +3-2×
+3-2×![]() ×
×![]() ×
×![]() =3,
=3,
∴ND2=3+1=4,
∴cos∠DMN=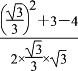 =-
=-![]() ,
,
即二面角D-PC-B的余弦值为-![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.
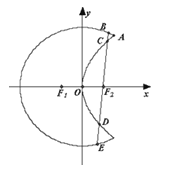
(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,D,E,F分别是B1C1,AB,AA1的中点.
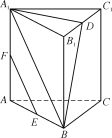
(1) 求证:EF∥平面A1BD;
(2) 若A1B1=A1C1,求证:平面A1BD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知![]() 三人分配奖金的衰分比为
三人分配奖金的衰分比为![]() ,若
,若![]() 分得奖金1000元,则
分得奖金1000元,则![]() 所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
A.![]() ,12800元B.
,12800元B.![]() ,12800元
,12800元
C.![]() ,10240元D.
,10240元D.![]() ,10240元
,10240元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月某城市国际马拉松赛正式举行,组委会对
月某城市国际马拉松赛正式举行,组委会对![]() 名裁判人员进(年龄均在
名裁判人员进(年龄均在![]() 岁到
岁到![]() 岁)行业务培训,现按年龄(单位:岁)进行分组统计:第
岁)行业务培训,现按年龄(单位:岁)进行分组统计:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如下:
,得到的频率分布直方图如下:
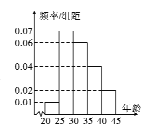
(1)若把这![]() 名裁判人员中年龄在
名裁判人员中年龄在![]() 称为青年组,其中男裁判
称为青年组,其中男裁判![]() 名;年龄在
名;年龄在![]() 的称为中年组,其中男裁判
的称为中年组,其中男裁判![]() 名.试完成
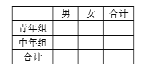
名.试完成![]() 列联表并判断能否在犯错误的概率不超过
列联表并判断能否在犯错误的概率不超过![]() 的前提下认为裁判员属于不同的组别(青年组或中年组)与性别有关系?
的前提下认为裁判员属于不同的组别(青年组或中年组)与性别有关系?
(2)培训前组委会用分层抽样调查方式在第![]() 组共抽取了
组共抽取了![]() 名裁判人员进行座谈,若将其中抽取的第
名裁判人员进行座谈,若将其中抽取的第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,若组委会决定从上述
,若组委会决定从上述![]() 名裁判人员中再随机选
名裁判人员中再随机选![]() 人参加新闻发布会,要求这
人参加新闻发布会,要求这![]() 组各选
组各选![]() 人,试求裁判人员
人,试求裁判人员![]() 不同时被选择的概率;
不同时被选择的概率;
附: 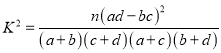
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为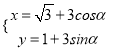 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场有一块等腰直角三角形的空地![]() ,其中斜边
,其中斜边![]() 的长度为400米.为迎接“五一”观光游,欲在边界
的长度为400米.为迎接“五一”观光游,欲在边界![]() 上选择一点
上选择一点![]() ,修建观赏小径
,修建观赏小径![]() ,其中
,其中![]() 分别在边界
分别在边界![]() 上,小径
上,小径![]() 与边界
与边界![]() 的夹角都为
的夹角都为![]() .区域
.区域![]() 和区域
和区域![]() 内种植郁金香,区域
内种植郁金香,区域![]() 内种植月季花.
内种植月季花.

(1)探究:观赏小径![]() 与
与![]() 的长度之和是否为定值?请说明理由;
的长度之和是否为定值?请说明理由;
(2)为深度体验观赏,准备在月季花区域内修建小径![]() ,当
,当![]() 点在何处时,三条小径
点在何处时,三条小径![]() 的长度和最小?
的长度和最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com