
【题目】已知数列![]() 的首项为
的首项为![]() ,且
,且![]() ,
, ![]() .
.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)由![]() 可得
可得![]() ,从而可得数列
,从而可得数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公差的等差数列;(2) 由(1)可知
为公差的等差数列;(2) 由(1)可知![]() ,,
,, ![]() ,利用裂项相消法可求得数列
,利用裂项相消法可求得数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1) ![]() ,
,
数列![]() 是以
是以![]() 为首项,以1为公差的等差数列;
为首项,以1为公差的等差数列;
(2)由(1)可知, ![]() ,
, ![]() ,
,
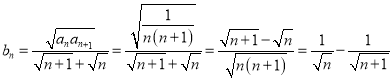 ,
,
![]()
![]() .
.
【方法点晴】本题主要考查等差数列的定义与通项公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
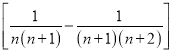 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
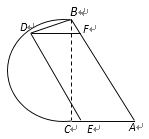
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,D,E,F分别是B1C1,AB,AA1的中点.
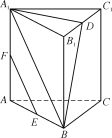
(1) 求证:EF∥平面A1BD;
(2) 若A1B1=A1C1,求证:平面A1BD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史。某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位; ![]() )数据,将数据分组如下表:
)数据,将数据分组如下表:
分组 | 频数 | 频率 |
| 4 | |
| 26 | |
| ||
| 28 | |
| 10 | |
| 2 | |
合计 | 100 |
(1)在答题卡上完成频率分布表;
(2)以表中的频率作为概率,估计重量落在![]() 中的概率及重量小于2.45的概率是多少?
中的概率及重量小于2.45的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知![]() 三人分配奖金的衰分比为
三人分配奖金的衰分比为![]() ,若
,若![]() 分得奖金1000元,则
分得奖金1000元,则![]() 所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
A.![]() ,12800元B.
,12800元B.![]() ,12800元
,12800元
C.![]() ,10240元D.
,10240元D.![]() ,10240元
,10240元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为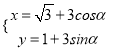 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某城市居民的月平均用电量情况,随机抽查了该城市100户居民的月平均用电量(单位:度),得到频率分布直方图(如图所示).数据的分组依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
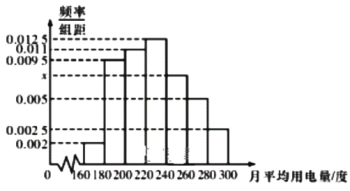
(1)求频率分布直方图中![]() 的值;
的值;
(2)求该城市所有居民月平均用电量的众数和中位数的估计值;
(3)在月平均用电量为![]() 的四组用户中,采用分层抽样的方法抽取
的四组用户中,采用分层抽样的方法抽取![]() 户居民,则应从月用电量在
户居民,则应从月用电量在![]() 居民中抽取多少户?
居民中抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com