
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
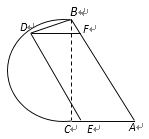
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
【答案】(1)![]() ;(2)
;(2)![]() 与
与![]() 重合.
重合.
【解析】分析:(1)解直角三角形BDC用![]() 表示
表示![]() 的长.(2)先利用正弦定理求出DF=4cosθsin(
的长.(2)先利用正弦定理求出DF=4cosθsin(![]() +θ), 再求出DE=AF=4-4
+θ), 再求出DE=AF=4-4![]() ,再利用三角函数求DE+DF的最大值.
,再利用三角函数求DE+DF的最大值.
详解:(1)连结DC.
在△ABC中,AC为2百米,AC⊥BC,∠A为![]() ,
,
所以∠CBA=![]() ,AB=4,BC=
,AB=4,BC=![]() .
.
因为BC为直径,所以∠BDC=![]() ,
,
所以BD=BC cosθ=![]() cosθ.
cosθ.
(2)在△BDF中,∠DBF=θ+![]() ,∠BFD=
,∠BFD=![]() ,BD=
,BD=![]() cosθ,
cosθ,
所以![]() ,
,
所以DF=4cosθsin(![]() +θ),
+θ),
且BF=4![]() ,所以DE=AF=4-4
,所以DE=AF=4-4![]() ,
,
所以DE+DF=4-4![]() +4
+4 ![]() sin(
sin(![]() +θ)=
+θ)=![]() sin2θ-cos2θ+3
sin2θ-cos2θ+3
=2 sin(2θ-![]() )+3.
)+3.
因为![]() ≤θ<
≤θ<![]() ,所以
,所以![]() ≤2θ-
≤2θ-![]() <
<![]() ,
,
所以当2θ-![]() =
=![]() ,即θ=
,即θ=![]() 时,DE+DF有最大值5,此时E与C重合.
时,DE+DF有最大值5,此时E与C重合.
答:当E与C重合时,两条栈道长度之和最大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.

表中![]() ,
,![]()
(Ⅰ)根据散点图判断,y=a+bx与y=c+d![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织了数学学科考试,随机抽取50名学生的成绩并制成频率分布直方图如图所示.

(1)求m的值,并估计高一年级所有学生数学成绩在![]() 分的学生所占的百分比;
分的学生所占的百分比;
(2)分别估计这50名学生数学成绩的平均数和中位数.(同一组中的数据以该组区间的中点值作代表,结果精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.

(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)具有较强的相关性,且两者之间有如下对应数据:
(单位:万元)具有较强的相关性,且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中的线性回归方程,当广告费支出为10万元时,预测销售额是多少?
参考数据: ![]() ,
,![]() ,
,![]() 。
。
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米两斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=4(单位:升),则输入k的值为( )

A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com