
(本题满分13分)
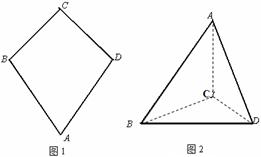
如图一,平面四边形 关于直线
关于直线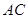 对称,
对称,
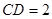 。
。
把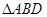 沿
沿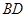 折起(如图二),使二面角
折起(如图二),使二面角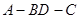 的余弦值等于
的余弦值等于 。对于图二,
。对于图二,

(Ⅰ)求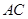 ;
;
(Ⅱ)证明: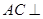 平面
平面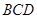 ;
;
(Ⅲ)求直线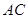 与平面
与平面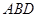 所成角的正弦值。
所成角的正弦值。
(Ⅰ)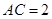 ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ)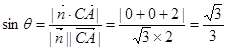 .
.
【解析】
试题分析:(I)取BD的中点E,先证得∠AEC就是二面角A-BD-C的平面角,再在△ACE中利用余弦定理即可求得AC;
(II)欲证线面垂直,转化为证明线线垂直,证明AC⊥BC,AC⊥CD即可;
(III)欲求直线AC与平面ABD所成角,先结合(I)中的垂直关系作出直线AC与平面ABD所成角,最后利用直角三角形中的边角关系即可求出所成角的正弦值.
解:(Ⅰ)取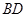 的中点
的中点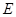 ,连接
,连接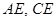 ,
,
由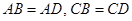 ,得:
,得: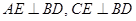
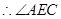 就是二面角
就是二面角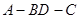 的平面角,
的平面角,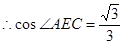 ……………2分
……………2分
在 中,
中,
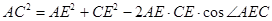

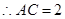 …………………………………4分
…………………………………4分
(Ⅱ)由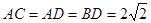 ,
,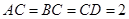
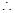
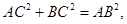
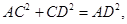
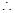
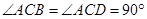
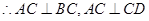 ,
又
,
又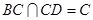
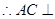 平面
平面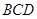 .……………8分
.……………8分
(Ⅲ)方法一:由(Ⅰ)知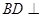 平面
平面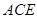
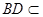 平面
平面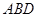
∴平面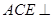 平面
平面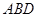 平面
平面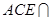 平面
平面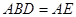 ,
,
作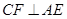 交
交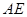 于
于 ,则
,则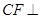 平面
平面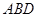 ,
,
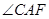 就是
就是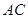 与平面
与平面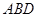 所成的角
所成的角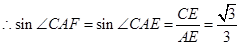 .……13分
.……13分
方法二:设点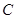 到平面
到平面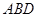 的距离为
的距离为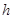 ,
,
∵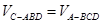
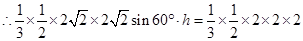
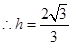 于是
于是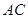 与平面
与平面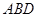 所成角
所成角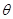 的正弦为
的正弦为 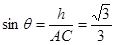 .
.
方法三:以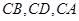 所在直线分别为
所在直线分别为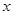 轴,
轴,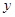 轴和
轴和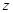 轴建立空间直角坐标系
轴建立空间直角坐标系 , 则
, 则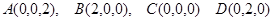 .
.
设平面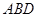 的法向量为
的法向量为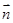
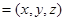 ,则
,则
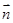
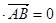 ,
, 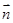
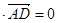 ,
,
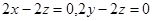
取 ,则
,则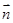
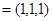 , 于是
, 于是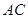 与平面
与平面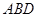 所成角
所成角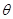 的正弦即
的正弦即
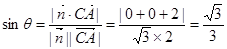 .
.
考点:本试题主要考查了余弦定理的运用,二面角、线面角的求法,线面垂直的判定,以及数形结合数学、空间想象能力或用向量解决立体几何问题的方法能力.
点评:解决该试题的关键是利用定义法得到二面角是该试题的突破口,并能结合三角形的与线订立的到边AC的长度。熟练运用线面垂直的判定定理和性质定理。


科目:高中数学 来源:2012届浙江省宁波万里国际学校高三上期中理科数学试卷(解析版) 题型:解答题
(本题满分13分) 的三个内角
的三个内角 依次成等差数列.
依次成等差数列.
(Ⅰ)若 ,试判断
,试判断 的形状;
的形状;
(Ⅱ)若 为钝角三角形,且
为钝角三角形,且 ,求
,求
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市朝阳区高三上学期期末考试理科数学 题型:解答题
(本题满分13分)
在锐角 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,
, ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(一级学校) 题型:解答题
(本题满分13分)
如图,在五面体ABCDEF中,FA 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD,AF=AB=BC=FE=
AD,AF=AB=BC=FE= AD.
AD.
(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com