
如果抛物线的顶点在原点,对称轴为x轴,焦点在直线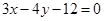 上,那么抛物线的方程是( )
上,那么抛物线的方程是( )
A.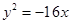 B.
B.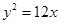
C.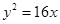 D.
D.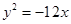
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
如果抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,那么抛物线的方程是
[ ]
查看答案和解析>>
科目:高中数学 来源:走向清华北大同步导读·高二数学(上) 题型:022
如果抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,那么该抛物线的方程为________.
查看答案和解析>>
科目:高中数学 来源:2014届河南安阳一中高二第一次阶段测试理科数学试卷(解析版) 题型:解答题
若抛物线的顶点在原点,其准线方程过双曲线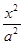 -
-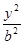 =1(
=1(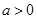 ,
,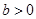 )的一个焦点,如果抛物线与双曲线交于
)的一个焦点,如果抛物线与双曲线交于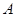 (
(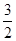 ,
,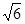 ),
),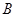 (
(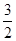 ,-
,-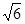 ),求两曲线的标准方程.
),求两曲线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分) 已知抛物线的顶![]() 点在原点,焦点在y轴上,过其上一点P(x0, y0)(x0≠0)
点在原点,焦点在y轴上,过其上一点P(x0, y0)(x0≠0)![]() 的切线方程为y-y0=-2x0 (x-x0).
的切线方程为y-y0=-2x0 (x-x0).
(Ⅰ)求抛物线方程;
(Ⅱ)斜率为k1的直线PA与抛物线的另一交点为A,斜率为k2的直线PB与抛物线的另一交点为B(A、B两点不同),且满足k2+λk1=0(λ≠0, λ≠-1),若![]() ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;
(Ⅲ)C、D是抛物线上的两个动点,若抛物线在C、D点处的切线互相垂直,直线CD是否过定点?如果是,求出定点坐标,如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com