练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将编号为1，2，3，4的四个小球，分别放入编号为1，2，3，4的四个盒子，每个盒子中有且仅有一个小球．若小球的编号与盒子的编号相同，得1分，否则得0分．记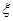为四个小球得分总和．
    （1）求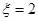时的概率；
    （2）求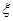的概率分布及数学期望．

    （1）；（2）详见解析.

    解析试题分析：（1）先确定时对应的事件，然后利用排列组合的相关知识求解；（2）将随机变量的可能取值确定下来，然后将对应的概率计算出来，列出分布列求出的数学期望与方差.
    试题解析：（1）时，则编号为1，2，3，4的四个小球中有且仅有两个小球的编号与盒子的编号相同，
    故，即时的概率为；                                     3分
    （2）的可能取值有、、、，                                               4分
    则，，
    ，，                       
    故的分布列如下表所示



    		 







                                                                                     8分
    ，                                            9分
    .                        10分
    考点：排列组合、随机变量的分布列、数学期望与方差

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某食品企业一个月内被消费者投诉的次数用表示，椐统计，随机变量的概率分布如下：


    		0
    		1
    		2
    		3
    p
    		0.1
    		0.3
    		2a
    		a
    （1）求a的值和的数学期望；
    （2）假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果．共选100名学生随机分成两个班，每班50名学生，其中一班采取“传统式教学法”，二班实行“三步式教学法”
    （Ⅰ）若全校共有学生2000名，其中男生1100名，现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查，应抽取多少名女生？
    （Ⅱ）下表1，2分别为实行“传统式教学”与“三步式教学”后的数学成绩：
    表1

    数学成绩
    		90分以下
    		90—120分
    		120—140分
    		140分以上
    频   数
    		15
    		20
    		10
    		5
    表2
    数学成绩
    		90分以下
    		90—120分
    		120—140分
    		140分以上
    频   数
    		5
    		40
    		3
    		2
    完成下面2×2列联表，并回答是否有99%的把握认为这两种教学法有差异.
    班  次
    		120分以下(人数)
    		120分以上(人数)
    		合计(人数)
    一班
    		 
    		 
    		 
    二班
    		 
    		 
    		 
    合计
    		 
    		 
    		 
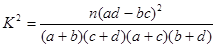    参考公式:,其中
    参考数据:
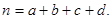
    P(K2≥k0)
    		0.40
    		0.25
    		0.10
    		0.05
    		0.010
    		0.005
    k0
    		0.708
    		1.323
    		2.706
    		3.841
    		6.635
    		7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各10件样品，测量产品中某种元素的含量（单位：毫克）.如图是测量数据的茎叶图：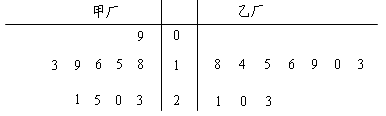

    规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品.
    （1）试用上述样本数据估计甲、乙两厂生产的优等品率；
    （2）从乙厂抽出的上述10件样品中，随机抽取3件，求抽到的3件样品中优等品数的分布列及其数学期望；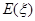
    （3）从甲厂的10件样品中有放回的随机抽取3件，也从乙厂的10件样品中有放回的随机抽取3件，求抽到的优等品数甲厂恰比乙厂多2件的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某大学一个专业团队为某专业大学生研究了多款学习软件，其中有A、B、C三种软件投入使用，经一学年使用后，团队调查了这个专业大一四个班的使用情况，从各班抽取的样本人数如下表

    班级
    		一
    		二
    		三
    		四
    人数
    		3
    		2
    		3
    		4
    （1）从这12人中随机抽取2人，求这2人恰好来自同一班级的概率．
    （2）从这12名学生中，指定甲、乙、丙三人为代表，已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是，且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为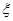，求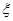的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究，对该校高二年级800名学生上学期期末语文和外语成绩，按优秀和不优秀分类得结果：语文和外语都优秀的有60人，语文成绩优秀但外语不优秀的有140人，外语成绩优秀但语文不优秀的有100人.
    （Ⅰ）能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系？
    （Ⅱ）将上述调查所得到的频率视为概率，从该校高二年级学生成绩中，有放回地随机抽取3名学生的成绩，记抽取的3 个成绩中语文，外语两科成绩至少有一科优秀的个数为X ，求X的分布列和期望E（x）.


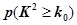         		0．010
         		0．005
         		0．001
     

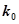         		6．635
         		7．879
         		10．828
     
    附：

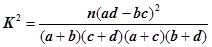
    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了调査某大学学生在某天上网的时间，随机对lOO名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果：
    表l:男生上网时间与频数分布表

    表2:女生上网时间与频数分布表

    (I)从这100名男生中任意选出3人，其中恰有1人上网时间少于60分钟的概率；
    (II)完成下面的2X2列联表，并回答能否有90%的把握认为“大学生上网时间与性别有关”？
    表3: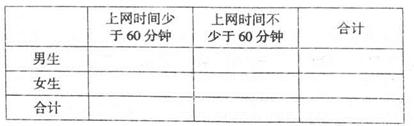
    •
    附：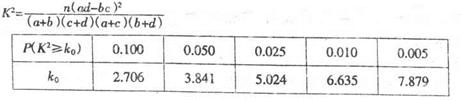

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4.
    (Ⅰ)从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；
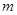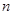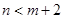    (Ⅱ)先从袋中随机取一个球，该球的编号为，将球放回袋中，然后再从袋中随机取一个球，该球的编号为，求的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：

     
    		男性
    		女性
    		合计
    反感
    		10
    		 
    		 
    不反感
    		 
    		8
    		 
    合计
    		 
    		 
    		30
    已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是．
    (Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果，不需要写求解过程)，并据此资料分析反感“中国式过马路 ”与性别是否有关？
    (Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望．
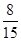    P(K2>k)
    		0.05
    		0.025
    		0.010
    		0.005
    k
    		3.841
    		5.024
    		6.635
    		7.879
    下面的临界值表供参考：
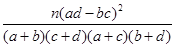    (参考公式：K2=，其中n="a+b+c+d)"

    查看答案和解析>>

    同步练习册答案