
如图所示,求图中曲边梯形的面积.
(只要求写出极限形式)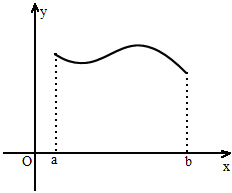
|
(1)分割:如图所示,将区间[a,b]任意分割成n个小区间,其分点记为:
(2) 近似代替:在每个小区间上任取一点,记为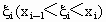 ,并记 ,并记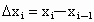 . .
以小区间长度  为底, 为底,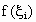 为高的小矩形面积为 为高的小矩形面积为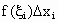 ,设小曲边梯形面积为 ,设小曲边梯形面积为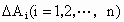 , ,
则有 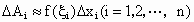 . .
(3) 求和:将所有n个小矩形面积加起来,得
(4) 取极限:如果分点的数目无限增多,且每个小区间的长度趋近于零时,和式①的极限存在,则和式①的极限就是所求曲边梯形的面积S.即 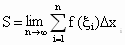 . .
|
解析: 利用无限逼近的思想先分割,用小矩形面积近似代替曲边梯形面积,分割越细,所求的近似值就越接近于曲边梯形面积的真实值,通过求极限,就可以得到所求面积的真实值,这种方法称之为微分法. |


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
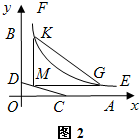
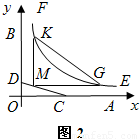
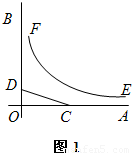
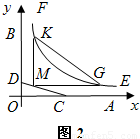
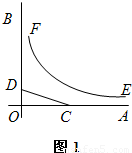
 如图1,OA,OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点M分别修建与OA,OB平行的栈桥MG、MK,且以MG、MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(0≤x≤20),曲线段EF的方程是xy=200(5≤x≤40),设点M的坐标为(s,t),记z=s•t.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度
如图1,OA,OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点M分别修建与OA,OB平行的栈桥MG、MK,且以MG、MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(0≤x≤20),曲线段EF的方程是xy=200(5≤x≤40),设点M的坐标为(s,t),记z=s•t.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南师大附中高三(下)第八次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:《三角函数》2013年高三一轮复习单元训练(北京师范大学附中)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com