
若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S=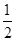 r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
科目:高中数学 来源: 题型:填空题
在平面几何里,有勾股定理:“设 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则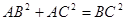 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
有一个奇数列1, 3, 5, 7, 9,…,现在进行如下分组:第一组含一个数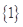 ,第二组含两个数
,第二组含两个数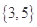 ,第三组含三个数
,第三组含三个数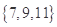 ,第四组含四个数
,第四组含四个数 ,…,现观察猜想每组内各数之和为
,…,现观察猜想每组内各数之和为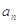 与其组的编号数
与其组的编号数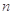 的关系为 .
的关系为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将正整数12分解成两个正整数的乘积有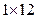 ,
, ,
,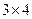 三种,其中
三种,其中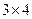 是这三种分解中,两数差的绝对值最小的,我们称
是这三种分解中,两数差的绝对值最小的,我们称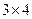 为12的最佳分解.当
为12的最佳分解.当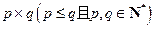 是正整数
是正整数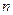 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数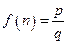 ,例如
,例如 .关于函数
.关于函数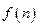 有下列叙述:①
有下列叙述:①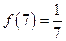 ,②
,②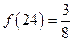 ,③
,③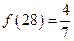 ,④
,④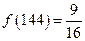 .其中正确的序号为 (填入所有正确的序号).
.其中正确的序号为 (填入所有正确的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com