
在数列{an}中,“an=2an-1,n=2,3,4,…”是“{an}是公比为2的等比数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
已知f(x)是偶函数,当x∈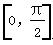 时,f(x)=xsin x,若a=f(cos 1),b=f(cos 2),c=f(cos 3),则a,b,c的大小关系为( )
时,f(x)=xsin x,若a=f(cos 1),b=f(cos 2),c=f(cos 3),则a,b,c的大小关系为( )
A.a<b<c B.b<a<c
C.c<b<a D.b<c<a
查看答案和解析>>
科目:高中数学 来源: 题型:
设F1,F2为椭圆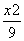 +
+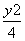 =1的两个焦点,P为椭圆上一点,已知P,F1,F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,则
=1的两个焦点,P为椭圆上一点,已知P,F1,F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,则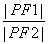 的值为( )
的值为( )
A.2 B.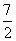 C.2或
C.2或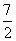 D.3或
D.3或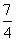
查看答案和解析>>
科目:高中数学 来源: 题型:
给出如下四个叙述:
①若“p且q”为假命题,则p,q均为假命题;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“∀x∈R,x2+1≥1”的否定是“∃x∈R,x2+1≤1”;
④在△ABC中,“A>B”是“sin A>sin B”的充要条件.
其中叙述不正确的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A,B,C,其中A={a1,a2,…,an},B={b1,b2,…,bn},C={c1,c2,…,cn},若A,B,C中的元素满足条件:c1<c2<…<cn,ak+bk=ck(k=1,2,3,…,n),则称M为“完并集合”.
(1)若M={1,x,3,4,5,6}为“完并集合”,则x的一个可能值为________.(写出一个即可)
(2)对于“完并集合”M={1,2,3,4,5,6,7,8,9,10,11,12},在所有符合条件的集合C中,其元素乘积最小的集合是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法正确的是( )
A.命题“存在x0∈R,x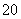 +x0+2 013>0”的否定是“任意x∈R,x2+x+2 013<0”
+x0+2 013>0”的否定是“任意x∈R,x2+x+2 013<0”
B.两个三角形全等是这两个三角形面积相等的必要条件
C.函数f(x)=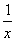 在其定义域上是减函数
在其定义域上是减函数
D.给定命题p,q,若“p且q”是真命题,则綈p是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com