【题目】已知函数g（x）= 
，则函数f（x）=g（lnx）﹣ln2x的零点个数为 ．
【答案】2
【解析】解：①如果lnx＞0，即x＞1时，
那么函数f（x）=g（lnx）﹣ln2x转化为函数f（x）=1﹣ln2x，令1﹣ln2x=0，得x=e，
即当x＞1时．函数f（x）=g（lnx）﹣ln2x的零点是e；
②如果lnx=0，即x=1时，
那么函数f（x）=g（lnx）﹣ln2x转化为函数f（x）=0﹣ln2x，令0﹣ln2x=0，得x=1，
即当x=1时．函数f（x）=g（lnx）﹣ln2x的零点是1；
③如果lnx＜0，即0＜x＜1时，
那么函数f（x）=g（lnx）﹣ln2x转化为函数f（x）=﹣1﹣ln2x，令﹣1﹣ln2x=0，无解，
即当0＜x＜1时．函数f（x）=g（lnx）﹣ln2x没有零点；
综上函数f（x）=g（lnx）﹣ln2x的零点个数为2．
所以答案是：2
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】如图所示，在直三棱柱ABC－A1B1C1中，AC⊥BC，AC＝BC＝CC1 ， M，N分别是A1B，B1C1的中点．
（1）求证：MN⊥平面A1BC；
（2）求直线BC1和平面A1BC所成的角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正四棱锥S﹣ABCD中，O为顶点在底面内的投影，P为侧棱SD的中点，且SO=OD，则直线BC与平面PAC的夹角是（ ）
A.30°
B.45°
C.60°
D.75°
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（x1 ， y1），B（x2 ， y2）均在抛物线上． 
（1）写出该抛物线的方程及其准线方程；
（2）当PA与PB的斜率存在且倾斜角互补时，求y1+y2的值及直线AB的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于二次函数y=﹣4x2+8x﹣3，
（1）指出图象的开口方向、对称轴方程、顶点坐标；
（2）求函数的最大值或最小值；
（3）写出函数的单调区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2+2ax+2，x∈[﹣5，5]．
（1）当a=﹣1时，求函数f（x）的最大值和最小值．
（2）函数y=f（x）在区间[﹣5，5]上是单调函数，求实数a的范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C1的参数方程为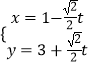 
（t为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2 
sin（θ+ 
）． （Ⅰ）求曲线C1与曲线C2的普通方程；
（Ⅱ）若点P的坐标为（﹣1，3），且曲线C1与曲线C2交于B，D两点，求|PB||PD|．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
