【题目】已知倾斜角为
的直线经过抛物线
的焦点
，与抛物线
相交于
、
两点，且
.
（1）求抛物线的方程；
（2）设
为抛物线上任意一点（异于顶点），过做倾斜角互补的两条直线
、
，交抛物线于另两点、
，记抛物线在点的切线
的倾斜角为
，直线
的倾斜角为
，求证：与互补.
名校课堂系列答案科目：高中数学 来源： 题型：
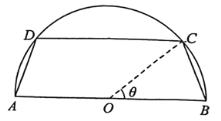
【题目】有一块半圆形的空地，直径
米，政府计划在空地上建一个形状为等腰梯形的花圃
，如图所示，其中
为圆心，
，
在半圆上，其余为绿化部分，设
.
（1）记花圃的面积为
，求的最大值；
（2）若花圃的造价为10元/米，在花圃的边
、
处铺设具有美化效果的灌溉管道，铺设费用为500元/米，两腰、不铺设，求
满足什么条件时，会使总造价最大.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一次考试结束后，随机抽查了某校高三（1）班5名同学的数学与物理成绩如下表：
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
（Ⅰ）分别求这5名同学数学与物理成绩的平均分与方差，并估计该班数学与物理成绩那科更稳定；
（Ⅱ）从以上5名同学中选2人参加一项活动，求选中的学生中至少有一个物理成绩高于90分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若曲线
在
处的切线与
轴平行，求
；
（2）已知
在
上的最大值不小于
，求的取值范围；
（3）写出所有可能的零点个数及相应的的取值范围.（请直接写出结论）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知空间中两条直线
，
所成的角为
，
为空间中给定的一个定点，直线
过点且与直线和直线所成的角都是
，则下列选项正确的是（ ）
A.当
时，满足题意的直线不存在
B.当
时，满足题意的直线有且仅有1条
C.当
时，满足题意的直线有且仅有2条
D.当
时，满足题意的直线有且仅有3条
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的3个红球和3个黑球，现从甲、乙两个盒内各任取2个球。
（1）求取出的4个球中没有红球的概率；
（2）求取出的4个球中恰有1个红球的概率；
（3）设
为取出的4个球中红球的个数，求
的分布列和数学期望。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四个命题：
①在回归分析中， 
可以用来刻画回归效果， 
的值越大，模型的拟合效果越好；
②在独立性检验中，随机变量
的值越大，说明两个分类变量有关系的可能性越大；
③在回归方程
中，当解释变量
每增加1个单位时，预报变量
平均增加1个单位；
④两个随机变量相关性越弱，则相关系数的绝对值越接近于1；
其中真命题是：
A. ①④ B. ②④ C. ①② D. ②③
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，(
).
（1）若曲线
在点
处的切线方程为
，求实数am的值；
（2）关于x的方程
能否有三个不同的实根？证明你的结论；
（3）若
对任意
恒成立，求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
