
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)写出![]() 所有可能的零点个数及相应的
所有可能的零点个数及相应的![]() 的取值范围.(请直接写出结论)
的取值范围.(请直接写出结论)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】从广安市某中学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() cm和
cm和![]() cm之间,将测量结果按如下方式分成八组:第一组
cm之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,...,第八组
,...,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人.
人.
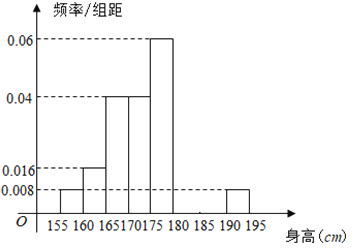
(1)求第七组的频率;
(2)估计该校![]() 名男生的身高的中位数。
名男生的身高的中位数。
(3)若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生,求抽出的两名男生是同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2ex﹣1(a≠0).
(1)求函数f(x)的单调区间;
(2)已知a>0且x∈[1,+∞),若函数f(x)没有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间[0,1]上的函数y=f(x)的图象如图所示.对满足0<x1<x2<1的任意x1,x2,给出下列结论:
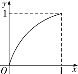
①f(x1)-f(x2)>x1-x2;
②f(x1)-f(x2)<x1-x2;
③x2f(x1)>x1f(x2);
④![]() .
.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为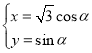 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上位于第一,二象限的两个动点,且
上位于第一,二象限的两个动点,且![]() ,射线
,射线![]() 交曲线
交曲线![]() 分别于
分别于![]() ,求
,求![]() 面积的最小值,并求此时四边形
面积的最小值,并求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 为抛物线
为抛物线![]() 上任意一点(异于顶点),过
上任意一点(异于顶点),过![]() 做倾斜角互补的两条直线
做倾斜角互补的两条直线![]() 、
、![]() ,交抛物线
,交抛物线![]() 于另两点
于另两点![]() 、
、![]() ,记抛物线
,记抛物线![]() 在点
在点![]() 的切线
的切线![]() 的倾斜角为
的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,求证:
,求证:![]() 与
与![]() 互补.
互补.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意
,且对任意![]() ,
,![]() (s,k,l,
(s,k,l,![]() )都有
)都有![]() ,则称数列
,则称数列![]() 为“T”数列.
为“T”数列.
(1)证明:正项无穷等差数列![]() 是“T”数列;
是“T”数列;
(2)记正项等比数列![]() 的前n项之和为
的前n项之和为![]() ,若数列
,若数列![]() 是“T”数列,求数列
是“T”数列,求数列![]() 公比的取值范围;
公比的取值范围;
(3)若数列![]() 是“T”数列,且数列
是“T”数列,且数列![]() 的前n项之和
的前n项之和![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com