
【题目】设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)证明:曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】解:(1)方程7x-4y-12=0可化为y=![]() x-3,
x-3,
当x=2时,y=![]() .
.
又f′(x)=a+![]() ,
,
于是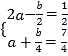 ,解得
,解得![]()
故f(x)=x-![]() .
.
(2)证明:设P(x0,y0)为曲线上任一点,由f′(x)=1+![]() 知,曲线在点P(x0,y0)处的切线方程为y-y0=(1+
知,曲线在点P(x0,y0)处的切线方程为y-y0=(1+![]() )·(x-x0),即y-(x0-
)·(x-x0),即y-(x0-![]() )=(1+
)=(1+![]() )(x-x0).
)(x-x0).
令x=0得,y=-![]() ,从而得切线与直线x=0,交点坐标为(0,-
,从而得切线与直线x=0,交点坐标为(0,- ![]() ).
).
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为![]() |-
|-![]() ||2x0|=6.
||2x0|=6.
曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,此定值为6.


科目:高中数学 来源: 题型:
【题目】已知数列{an}中an= ![]() (n∈N*),将数列{an}中的整数项按原来的顺序组成数列{bn},则b2018的值为( )
(n∈N*),将数列{an}中的整数项按原来的顺序组成数列{bn},则b2018的值为( )
A.5035
B.5039
C.5043
D.5047
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技创新公司在第一年年初购买了一台价值昂贵的设备,该设备的第1年的维护费支出为20万元,从第2年到第6年,每年的维修费增加4万元,从第7年开始,每年维修费为上一年的125%.
(1)求第n年该设备的维修费![]() 的表达式;
的表达式;
(2)设![]() ,若
,若![]() 万元,则该设备继续使用,否则须在第n年对设备更新,求在第几年必须对该设备进行更新?
万元,则该设备继续使用,否则须在第n年对设备更新,求在第几年必须对该设备进行更新?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点O为极点,
,(t为参数),在以原点O为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 两点的极坐标分别为.
两点的极坐标分别为.![]()
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题只理科做,满分14分)如图,已知![]() 平面
平面![]() ,
,![]() ,△
,△![]() 是正三角形,
是正三角形,![]() ,且
,且![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A.在等差数列{an}中,若ap+aq=ar+aδ , 则p+q=r+δ
B.已知数列{an}的前n项和为Sn , 若{an}是等比数列,则Sk , S2k﹣Sk , S3k﹣S2k也是等比数列
C.在数列{an}中,若ap+aq=2ar , 则ap , ar , aq成等差数列
D.在数列{an}中,若ap?aq=a ![]() ,则ap , ar , aq成等比数列
,则ap , ar , aq成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且a1=1,an+12=Sn+1+Sn .
(1)求{an}的通项公式;
(2)设bn=a2n﹣1![]() , 求数列{bn}的前n项和Tn .
, 求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com