
【题目】在等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.现
的中点.现![]() 沿
沿![]() 边折起成如图四棱锥
边折起成如图四棱锥![]() ,
,![]() 为
为![]() 中点.
中点.
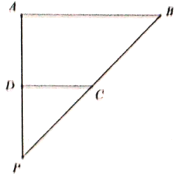
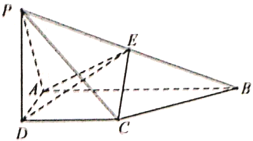
(1)证明:![]() 面
面![]() ;
;
(2)当![]() 时,求二面角
时,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 中点
中点![]() ,由中位线定理可证
,由中位线定理可证![]() ,
,![]() ,由面面平行的判定定理可证面
,由面面平行的判定定理可证面![]() 面
面![]() ,由面面平行的性质定理即可证得
,由面面平行的性质定理即可证得![]() 面
面![]() ;
;
(2)连结![]() ,由勾股定义证得
,由勾股定义证得![]() ,由线面垂直的判定定理证得
,由线面垂直的判定定理证得![]() 面
面![]() ,即可说明
,即可说明![]() ,
,![]() ,
,![]() 两两互相垂直,进而以点
两两互相垂直,进而以点![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 正方向建立空间直角坐标系,再分别表示点C,A,P,B,E的坐标,进而求面
正方向建立空间直角坐标系,再分别表示点C,A,P,B,E的坐标,进而求面![]() 与面
与面![]() 的法向量,再由数量积中求夹角的计算公式求得余弦值,最后观察下结论.
的法向量,再由数量积中求夹角的计算公式求得余弦值,最后观察下结论.
折前:![]() ,
,![]() ,折后:
,折后:![]() ,
,![]()
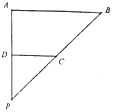

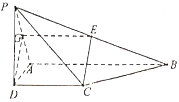
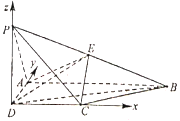
(1)证明:(法一)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() ,
,![]() ,又
,又![]() ,
,
∴面![]() 面
面![]() ,又
,又![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(法二)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(2)连结![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,
,
由![]() 即
即![]() 得
得![]()
又![]() ,
,![]() ,∴
,∴![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,![]() 两两互相垂直,以点
两两互相垂直,以点![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 正方向建如图系.
正方向建如图系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
设![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() ,由
,由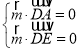 即
即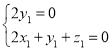 ,取
,取![]() ;
;
由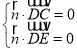 ,即
,即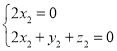 ,取
,取![]() .则
.则![]() ,
,
又二面角![]() 为钝角.故二面角
为钝角.故二面角![]() 的余弦值为
的余弦值为![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() ,
,![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() ,
,![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
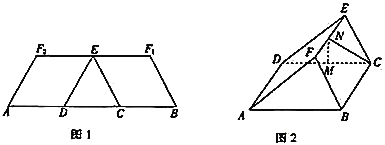
(1)证明:![]() 平面
平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级三个班共有学生120名,这三个班的男女生人数如下表所示,已知在全年级中随机抽取1名学生,抽到二班女生的概率是0.2,则![]() _________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
_________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
一班 | 二班 | 三班 | |
女生人数 | 20 |
|
|
男生人数 | 20 | 20 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间[0,1]上的函数y=f(x)的图象如图所示.对满足0<x1<x2<1的任意x1,x2,给出下列结论:
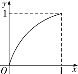
①f(x1)-f(x2)>x1-x2;
②f(x1)-f(x2)<x1-x2;
③x2f(x1)>x1f(x2);
④![]() .
.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]()
![]() ,对于
,对于![]() ,
,![]() ,定义A与B的差为
,定义A与B的差为![]() ;A与B之间的距离为
;A与B之间的距离为![]() .
.
(I)若![]() ,试写出所有可能的A,B;
,试写出所有可能的A,B;
(II)![]() ,证明:
,证明:
(i)![]() ;
;
(ii)![]()
![]()
![]() 三个数中至少有一个是偶数;
三个数中至少有一个是偶数;
(III)设![]() ,
,![]() 中有m(
中有m(![]() ,且为奇数)个元素,记P中所有两元素间距离的平均值为
,且为奇数)个元素,记P中所有两元素间距离的平均值为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 为抛物线
为抛物线![]() 上任意一点(异于顶点),过
上任意一点(异于顶点),过![]() 做倾斜角互补的两条直线
做倾斜角互补的两条直线![]() 、
、![]() ,交抛物线
,交抛物线![]() 于另两点
于另两点![]() 、
、![]() ,记抛物线
,记抛物线![]() 在点
在点![]() 的切线
的切线![]() 的倾斜角为
的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,求证:
,求证:![]() 与
与![]() 互补.
互补.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣x+1,g(x)=ex﹣ax,a∈R.
(Ⅰ)求f(x)的最小值;
(Ⅱ)若g(x)≥1在R上恒成立,求a的值;
(Ⅲ)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
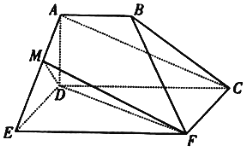
【题目】如图所示,空间几何体![]() 中,四边形
中,四边形![]() 是梯形,四边形
是梯形,四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)求证: ![]() ;
;
(2)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(3)在(2)的条件下,求空间几何体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com