
| x | 6 | 8 | 10 | 12 |
| y | 3 | 4 | 6 | 7 |
分析 (1)作出利用最小二乘法来求线性回归方程的系数的量,求出横标和纵标的平均数,求出系数,再求出a的值.得到回归直线方程.
(2)由回归直线方程预测,记忆力为9的同学的判断力约为5.
解答 解:(1)∵$\overline{x}$=9,$\overline{y}$=5,
$\sum_{i=1}^{4}$xiyi=6×3+8×4+10×6+12×7=194,$\sum_{i=1}^{4}$xi2=344
∴b=0.7,
∴a=5-0.7×9=-1.3
故线性回归方程为y=0.7x-1.3
(2)由回归直线方程预测,记忆力为9的同学的判断力约为y=0.7×9-1.3=5.
点评 本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法做出线性回归方程的系数.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{4}$ | B. | $\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{10}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
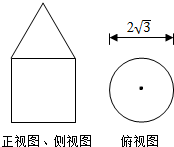 如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为$\sqrt{3}$的圆(包括圆心).则该组合体的表面积(各个面的面积的和)等于21π.
如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为$\sqrt{3}$的圆(包括圆心).则该组合体的表面积(各个面的面积的和)等于21π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,点O为作简谐振动的物体的平衡位置,取向右方向为正方向,若振幅为3cm,周期为4s,且物体向右运动到距平衡位置最远处时开始计时.则该物体10s时刻的路程为-3cm.
如图,点O为作简谐振动的物体的平衡位置,取向右方向为正方向,若振幅为3cm,周期为4s,且物体向右运动到距平衡位置最远处时开始计时.则该物体10s时刻的路程为-3cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com