
【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 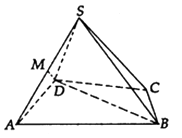
(1)求证:SA⊥BD;
(2)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC.
【答案】
(1)如图示:

证明:设BD中点为O,连接OC,OE,则由BC=CD知,CO⊥BD,
又已知SC⊥BD,SC⊥CO=C,所以BD⊥平面SOC,
∵△ABD是正三角形,∴AO是BD的中垂线,
故A、O、C在同一直线上,
故平面SAC即平面SOC,
由BD⊥OC,BD⊥SC,得BD⊥平面SAC,
故SA⊥BD
(2)证明:取AB中点N,连接DM,MN,DN,
∵M是SA的中点,∴MN∥BE,
∵△ABD是正三解形,∴DN⊥AB,
∵∠BCD=120°得∠CBD=30°,∴∠ABC=90°,即BC⊥AB,
所以ND∥BC,所以平面MND∥平面BSC,
故DM∥平面SBC.
【解析】(1)根据线面垂直以及线段的垂直平分线的性质证明即可;(2)由线线平行到面面平行从而推出线面平行即可.
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

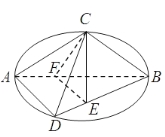
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足(1﹣a1008)5+2016(1﹣a1008)=1,(1﹣a1009)5+2016(1﹣a1009)=﹣1,数列{an}的前n项和记为Sn , 则( )
A.S2016=2016,a1008>a1009
B.S2016=﹣2016,a1008>a1009
C.S2016=2016,a1008<a1009
D.S2016=﹣2016,a1008<a1009
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线C1的参数方程为 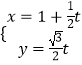 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.
(Ⅰ)写出C1的普通方程和C2的直角坐标方程;
(Ⅱ)直线C1与曲线C2相交于A,B两点,点M(1,0),求||MA|﹣|MB||.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若函数![]() ,
, ![]() 的最小值为-16,求实数
的最小值为-16,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上是单调减函数,求实数
上是单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]()
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两个不同点,求
两个不同点,求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 有无数对互相垂直的直线
有无数对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数为f'(x),且f'(x)<f(x)对任意的x∈R恒成立,则下列不等式均成立的是( )
A.f(ln2)<2f(0),f(2)<e2f(0)
B.f(ln2)>2f(0),f(2)>e2f(0)
C.f(ln2)<2f(0),f(2)>e2f(0)
D.f(ln2)>2f(0),f(2)<e2f(0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com