
分析 (I)先求出击中各环的频率,在作图;
(II)事件C包含3种情况,每一种情况都按条件概率计算,然后再相加即可;
(III)按条件概率计算出ξ分别为0,1,2的概率得出分布列,再计算数学期望.
解答 解:(I)甲的频率分布条形图如图1:
乙的频率分布条形图如图2:
(II)由甲乙运动员的设计环数条形图可知P甲(8环)=0.2,P甲(9环)=0.45,P甲(10环)=0.35,
P乙(8环)=0.25,P乙(9环)=0.4,P乙(10环)=0.35,
∴甲击中9环乙击中8环的概率为0.45×0.25=0.1125,
甲击中10环乙击中8环的概率为0.35×0.25=0.0875,
甲击中10环乙击中9环的概率为0.35×0.4=0.14.
∴P(C)=0.1125+0.0875+0.14=0.34.
(II)ξ的取值为0,1,2.
P(ξ=0)=0.65×0.65=0.4225,P(ξ=1)=0.65×0.35+0.35×0.65=0.455,P(ξ=2)=0.35×0.35=0.1225,
ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | 0.4225 | 0.455 | 0.1225 |
点评 本题考查了频率分布图的制作,条件概率计算,离散性随机变量的分布列和数学期望,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,A(2,0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)长轴右端点,点B,C在椭圆C上,BC过椭圆O,$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{AC}$|,M,N为椭圆上异于A,B的不同两点,∠MCN的角平分线垂直于x轴.
如图,A(2,0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)长轴右端点,点B,C在椭圆C上,BC过椭圆O,$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{AC}$|,M,N为椭圆上异于A,B的不同两点,∠MCN的角平分线垂直于x轴.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
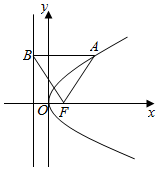 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若△ABF为等边三角形,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若△ABF为等边三角形,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com