
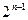 +1 (n∈N*), 则算过关.
+1 (n∈N*), 则算过关.| ξ | 0 | 1 | 2 | 3 |
| P | ||||
| ξ | 0 | 1 | 2 | 3 |
| P | ||||
| ξ | 0 | 1 | 2 | 3 |
| P |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
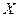 的分布列。
的分布列。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
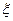 ,求
,求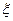 的分布列和期望。
的分布列和期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中样本橘子树产量的分组区间为[5,15),[15,25),[25,35),[35,45),[45,55),由此得到表1和图1的所示内容,其中表1是施用A种肥料后橘子树产量的频数分布表,图1是施用B种肥料后橘子树产量的频率分布直方图.
中样本橘子树产量的分组区间为[5,15),[15,25),[25,35),[35,45),[45,55),由此得到表1和图1的所示内容,其中表1是施用A种肥料后橘子树产量的频数分布表,图1是施用B种肥料后橘子树产量的频率分布直方图.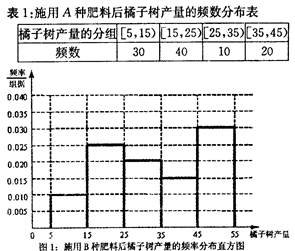
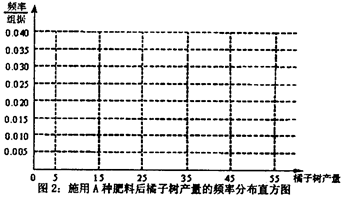
 比较施用A、B两种肥料对橘子树产量提高的影响那种更大,理由是什么?
比较施用A、B两种肥料对橘子树产量提高的影响那种更大,理由是什么?| 橘子树产量的分组 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) |
| 频数 | | | | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 0分)
0分) 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
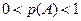
| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com