
如图1,直角梯形 中,
中, ,
, 分别为边
分别为边 和
和 上的点,且
上的点,且 ,
, .将四边形
.将四边形 沿
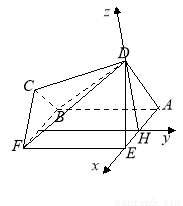
沿 折起成如图2的位置,使
折起成如图2的位置,使 .
.
(1)求证:
 平面
平面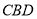 ;
;
(2)求平面 与平面
与平面 所成锐角的余弦值.
所成锐角的余弦值.

(1)见解析;(2) 。
。
【解析】
试题分析:(1)取DE中点G,连接FG,AG, 平面
平面 ,只需证平面AFG∥平面CBD,又
,只需证平面AFG∥平面CBD,又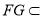 平面
平面 ,
, 平面
平面 ,故只需证
,故只需证 ∥平面CBD,
∥平面CBD, ∥平面CBD即可;
∥平面CBD即可;
(2)要求平面 与平面
与平面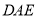 所成锐角的余弦值,需找两平面的法向量,取
所成锐角的余弦值,需找两平面的法向量,取 中点为H,连接DH,可证
中点为H,连接DH,可证 , 故以
, 故以 中点H为原点,
中点H为原点, 为
为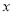 轴建立如图所示的空间直角坐标系,易知
轴建立如图所示的空间直角坐标系,易知 是平面
是平面 的一个法向量,由
的一个法向量,由 可得平面
可得平面 的一个法向量为
的一个法向量为 ,然后由空间两向量夹角公式去求平面
,然后由空间两向量夹角公式去求平面 与平面
与平面 所成锐角的余弦值。
所成锐角的余弦值。
试题解析:(1)证明:取DE中点G,连接FG,AG,CG.因为 CF DG,所以FG∥CD.因为 CG
DG,所以FG∥CD.因为 CG AB, ,
AB, ,
所以AG∥BC.所以平面AFG∥平面CBD, 所以 AF∥平面CBD.
(2)解: 取 中点为H,连接DH.
中点为H,连接DH. ,
, ,
,
 .
. ,
, .
.
以 中点H为原点,
中点H为原点, 为
为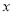 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则 ,
, ,
, ,
, 所以
所以 的中点坐标为
的中点坐标为 因为
因为 ,所以
,所以 易知
易知 是平面
是平面 的一个法向量,
的一个法向量, 设平面
设平面 的一个法向量为
的一个法向量为
由
令 则
则 ,
, ,
,
 ,
,
所以面 与面
与面 所成角的余弦值为
所成角的余弦值为 .
.
考点:(1)空间线面平行、面面平行、线面垂直判定定理的应用;(2)空间两平面夹角的定义、平面法向量的定义的应用;(3)空间向量的基本运算。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ文科数学试卷(解析版) 题型:选择题
如图所示,图中有5组数据,去掉 组数据后(填字母代号),剩下的4组数据的线性相关性最大( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届云南省高二下学期第二次月考文科数学试卷(解析版) 题型:选择题
记集 和集
和集 表示的平面区域分别为
表示的平面区域分别为 .若在区域
.若在区域 内任取一点
内任取一点 ,则点
,则点 落在区域
落在区域 的概率为( )
的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届云南省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,则曲线
轴的正半轴建立平面直角坐标系,则曲线 的直角坐标方程为 .
的直角坐标方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com