
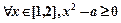 ”,命题q:“
”,命题q:“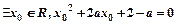 ”,若“p
”,若“p q”为真命题,求实数a的取值范围。
q”为真命题,求实数a的取值范围。 考前必练系列答案
考前必练系列答案科目:高中数学 来源:不详 题型:单选题
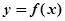 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足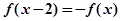 对一切
对一切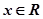 恒成立,当
恒成立,当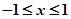 时,
时,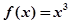 。则下列四个命题中正确的命题是
。则下列四个命题中正确的命题是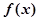 是以4为周期的周期函数;②
是以4为周期的周期函数;②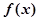 在
在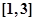 上的解析式为
上的解析式为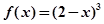 ;③
;③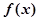 的图象的对称轴中有
的图象的对称轴中有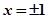 ;④
;④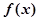 在
在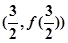 处的切线方程为
处的切线方程为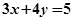 。
。| A.①②③ | B.②③④ | C.①③④ | D.①②③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.命题“若p,则q”与命题“若非q,则非p”互为逆否命题 |
B.命题q:?x∈R,sinx-cosx= 。则¬q是假命题 。则¬q是假命题 |
C.为得到函数y=sin(2x- )图象,只需把函数y=sin(2x+ )图象,只需把函数y=sin(2x+ )的图象向右平移 )的图象向右平移 个长度单位 个长度单位 |
D.若函数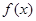 的导数为 的导数为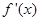 , , 为 为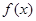 的极值的充要条件是 的极值的充要条件是 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
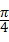 ,
,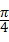 ]上是增函数;④f(x)的图象关于直线x=
]上是增函数;④f(x)的图象关于直线x= 对称.
对称.| A.①②④ | B.①③ |
| C.②③ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com