
在直角坐标系 中,已知点
中,已知点 ,
, ,
, ,点
,点 在
在 三边围成的区域(含边界)上,且
三边围成的区域(含边界)上,且 .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)用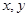 表示
表示 ,并求
,并求 的最小值.
的最小值.
(1)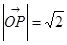 ,(2)
,(2) 的最小值-1.
的最小值-1.
解析试题分析:(1)向量的坐标运算主要是利用加、减、数乘运算法则进行的.若已知有向线段两端点的的坐标,则应先求出向量的坐标,解题过程中要注意方程的思想的运用及运算法则的正确使用;(2)利用线性规划求目标函数的最值一般步骤:一画、二移、三求,其关键是准确的作出可行域,理解目标函数的意义;(3)在线性约束条件下,线性目标函数只有在可行域的顶点或者边界上取得最值.在解答选择题和填空题时可以根据可行域的顶点直接进行检验.
试题解析:解(Ⅰ)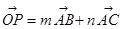
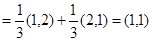 ,
,
∴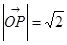 ....................5分
....................5分
由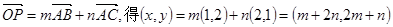 ,
,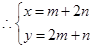 ,
,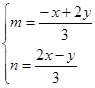 ,
,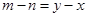
 8分
8分
设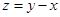 ,直线
,直线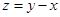 过点
过点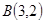 时,
时,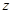 取得最小值-1,即
取得最小值-1,即 的最小值-1
的最小值-1
考点:(1)向量的坐标表示;(2)线性目标函数的最值.


科目:高中数学 来源: 题型:解答题
某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告,能给公司带来的收益分别为0.3 万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产A,B两种产品,生产每吨产品所需的劳动力和煤、电耗如下表:
已知生产每吨A产品的利润是5万元,生产每吨B产品的利润是10万元,现因条件限制,该企业仅有劳动力300个,煤360 t,并且供电局只能供电200 kW,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设x,y满足约束条件 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设a,b,c是正数,P=a+b-c,Q=b+c-a,R=c+a-b,则“P·Q·R>0”是“P,Q,R同时大于零”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com