
设x,y满足约束条件 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求 的最小值.
的最小值.
(1)10;(2)4
解析试题分析:(1)如图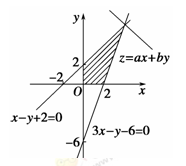
先在直角坐标系中画出各直线方程,再用特殊点代入法判断各不等式表示的平面区域,其公共部分即为不等式组表示的平面区域,用分割法即可求出其面积。(2)画出目标函数线,平移使其经过可行域当目标函数线的纵截距最大时, 取得最大值,求出满足条件的此点坐标代入目标函数。用基本不等式求
取得最大值,求出满足条件的此点坐标代入目标函数。用基本不等式求 的最小值。
的最小值。
试题解析:解:(1)不等式表示的平面区域如图所示阴影部分. 3分
联立 得点C坐标为(4,6)
得点C坐标为(4,6)
平面区域的面积 . 6分
. 6分
(2)当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点C(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大值4,即4a+6b=4,
即 . 9分
. 9分
所以
等号成立当且仅当 时取到.
时取到.
故 的最小值为4. 12分
的最小值为4. 12分
考点:1线性规划;2基本不等式。


科目:高中数学 来源: 题型:解答题
某营养师要为某个儿童预订午餐和晚餐,已知一个单位的午餐含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 ;一个单位的晚餐含
;一个单位的晚餐含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 .另外,该儿童这两餐需要的营养中至少含
.另外,该儿童这两餐需要的营养中至少含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 .如果一个单位的午餐、晚餐的费用分别是
.如果一个单位的午餐、晚餐的费用分别是 元和
元和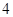 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.求该公司从每天生产的甲、乙两种产品中,可获得的最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1kg、B原料2kg;生产乙产品1桶需耗A原料2kg,B原料1kg.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12kg.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com