
函数 .
.
(1)若 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;
(2)若 ,若函数
,若函数 在 [1,3]上恰有两个不同零点,求实数
在 [1,3]上恰有两个不同零点,求实数 的取值范围.
的取值范围.
(1)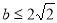 ;(2)2-2ln2<k
;(2)2-2ln2<k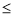 3-2ln3
3-2ln3
【解析】
试题分析:(1)由当a=-2时,函数h(x)在其定义域(0,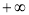 )内是增函数,可得
)内是增函数,可得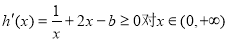 恒成立,从而通过分离参数转化为求函数的最小值处理.
恒成立,从而通过分离参数转化为求函数的最小值处理.
(2)函数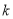
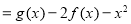 在[1,3]上恰有两个不同的零点等价于方程
在[1,3]上恰有两个不同的零点等价于方程 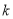 =
=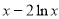 ,在[1,3]上恰有两个相异实根; 等价于函数
,在[1,3]上恰有两个相异实根; 等价于函数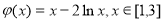 的图象与直线
的图象与直线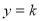 有两个不同的交点,利用函数的导数求出函数
有两个不同的交点,利用函数的导数求出函数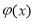 的单调区间与极值,就可画出
的单调区间与极值,就可画出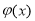 的大致图象,通过图象观查可知
的大致图象,通过图象观查可知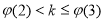 从而求得k的取值范围.
从而求得k的取值范围.
试题解析:(1)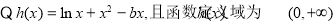 ,则:
,则:
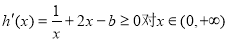 恒成立,
恒成立, 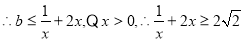 ,
,
(当且仅当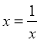 时,即
时,即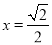 时,取等号),
时,取等号),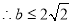
(2)函数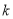
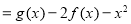 在[1,3]上恰有两个不同的零点等价于方程
在[1,3]上恰有两个不同的零点等价于方程 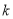 =
=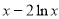 ,在[1,3]上恰有两个相异实根.
,在[1,3]上恰有两个相异实根.
令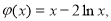 则
则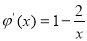 ;当
;当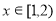 ,
,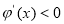 ;当
;当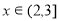 时,
时,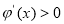 ;所以
;所以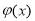 在[1,2]上是单调递减函数,在(2,3]上是单调递增函数;故
在[1,2]上是单调递减函数,在(2,3]上是单调递增函数;故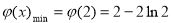 ,又
,又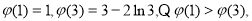 如图,故只需
如图,故只需 ,所以有:2-2ln2<k
,所以有:2-2ln2<k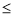 3-2ln3
3-2ln3
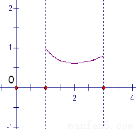
考点:1.由函数单调性求参数的取值范围;2.函数图象与零点.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:2015届山东省高二下学期期中检测文科数学试卷(解析版) 题型:选择题
已知y与x线性相关,其回归直线的斜率的估计值为1.23,样本的中心点为(4,5),则其回归直线方程为( )
A.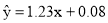 B.
B.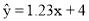
C.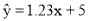 D.
D.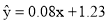
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
下列命题中,真命题是( )
A.?x∈R,ex≤0
B.?x∈R,2x>x2
C.a+b=0的充要条件是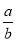 =-1
=-1
D.a>1,b>1是ab>1的充分条件
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时, 在
在 上是“凸函数”.则
上是“凸函数”.则 在
在 上 ( )
上 ( )
A.既有极大值,也有极小值 B.既有极大值,也有最小值
C.有极大值,没有极小值 D.没有极大值,也没有极小值
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:选择题
已知x=lnπ,y=log52,z= ,则( )
,则( )
A.x<y<z B.z<x<y C.z<y<x D.y<z<x
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:填空题
若双曲线 的左、右焦点分别为F1,F2,线段F1F2被抛物线
的左、右焦点分别为F1,F2,线段F1F2被抛物线 的焦点分成5:3两段,则此双曲线的离心率为______.
的焦点分成5:3两段,则此双曲线的离心率为______.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:解答题
设椭圆 的焦点在
的焦点在 轴上.
轴上.
(1)若椭圆 的焦距为1,求椭圆
的焦距为1,求椭圆 的方程;
的方程;
(2)设 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 上的第一象限内的点,直线
上的第一象限内的点,直线 交
交 轴与点
轴与点 ,并且
,并且 ,证明:当
,证明:当 变化时,点
变化时,点 在某定直线上.
在某定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com