
已知数列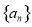 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若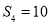 ,
,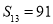 .
.
(1)求 ;
;
(2)若数列{Mn}满足条件: 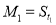 ,当
,当 时,
时,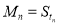 -
-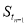 ,其中数列
,其中数列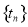 单调递增,且
单调递增,且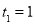 ,
,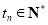 .
.
①试找出一组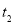 ,
,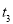 ,使得
,使得 ;
;
②证明:对于数列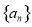 ,一定存在数列
,一定存在数列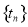 ,使得数列
,使得数列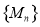 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
(1)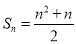 (2)①
(2)①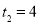 ,
,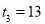 ②详见解析
②详见解析
【解析】
试题分析:(1)求等比数列前n项和,一般利用待定系数法,即求出首项及公差即可:由 ,
,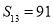 ,得
,得 ,解得
,解得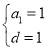 ,所以
,所以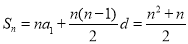 (2)①新定义问题,解题思路就是按定义归纳转化条件:因为
(2)①新定义问题,解题思路就是按定义归纳转化条件:因为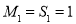 ,依次设
,依次设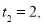
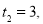
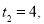 验证
验证 是否有解
是否有解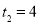 ,
,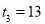 是第一组满足题意,②由①知
是第一组满足题意,②由①知 ,
,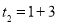 ,
, ,则
,则 ,
,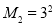 ,
,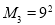 ,本题也是在归纳基础上探求解法:一般的取
,本题也是在归纳基础上探求解法:一般的取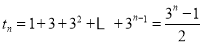 ,此时
,此时 ,
, ,则
,则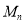 =
=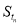 -
- =
=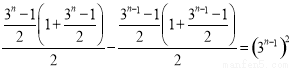 ,所以
,所以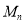 为一整数平方.
为一整数平方.
试题解析:(1)设数列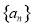 的首项为
的首项为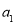 ,公差为
,公差为 ,
,
由 ,
,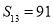 ,得
,得 , 2分
, 2分
解得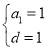 ,
,
所以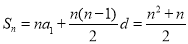 4分
4分
(2)①因为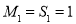 ,
,
若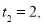
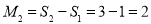 ,
,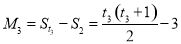 ,
,
因为 ,
,
所以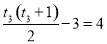 ,
,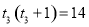 ,此方程无整数解; 6分
,此方程无整数解; 6分
若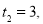
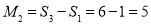 ,
,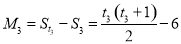 ,
,
因为 ,
,
所以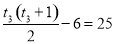 ,
, ,此方程无整数解; 8分
,此方程无整数解; 8分
若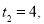
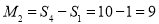 ,
,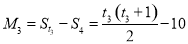 ,
,
因为 ,
,
所以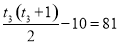 ,
, ,解得
,解得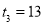 ,
,
所以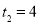 ,
,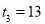 满足题意 10分
满足题意 10分
②由①知 ,
,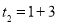 ,
, ,则
,则 ,
,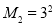 ,
,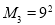 ,
,
一般的取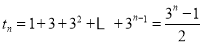 , 13分
, 13分
此时 ,
, ,
,
则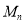 =
=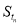 -
- =
=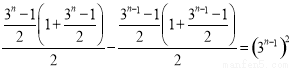 ,
,
所以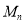 为一整数平方.
为一整数平方.
因此存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方. 16分
中的各数均为一个整数的平方. 16分
考点:求等差数列和项,归纳探求新定义问题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年安徽省蚌埠市高一上学期期中考试数学试卷(解析版) 题型:选择题
下列四个图像中,是函数图像的是 ( )
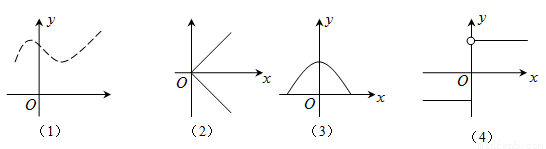
A.(1)
B.(1)、(3)、(4)
C.(1)、(2)、(3)
D.(3)、(4)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试文科数学试卷(解析版) 题型:解答题
已知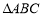 的内角
的内角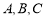 的对边分别为
的对边分别为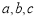 ,
, .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)若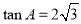 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试理科数学试卷(解析版) 题型:解答题
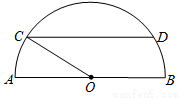
如图是一个半圆形湖面景点的平面示意图.已知 为直径,且
为直径,且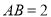 km,
km, 为圆心,
为圆心,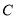 为圆周上靠近
为圆周上靠近 的一点,
的一点, 为圆周上靠近
为圆周上靠近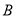 的一点,且
的一点,且 ∥
∥ .现在准备从
.现在准备从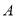 经过
经过 到
到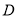 建造一条观光路线,其中
建造一条观光路线,其中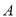 到
到 是圆弧
是圆弧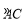 ,
, 到
到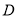 是线段
是线段 .设
.设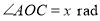 ,观光路线总长为
,观光路线总长为 .
.
(1)求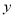 关于
关于 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)为了分析某次考试数学成绩情况,用简单随机抽样从某班中抽取25名学生的成绩(百分制)作为样本,得到频率分布表如下:
分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 2 | 3 | 9 | a | 1 |
频率 | 0.08 | 0.12 | 0.36 | b | 0.04 |
(Ⅰ)求样本频率分布表中a,b的值,并根据上述频率分布表,在下表中作出样本频率分布直方图;
(Ⅱ)计算这25名学生的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)从成绩在[50,70)的学生中任选2人,求至少有1人的成绩在[60,70)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com