
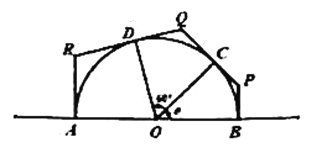
【题目】为美化城市环境,相关部门需对一半圆形中心广场进行改造出新,为保障市民安全,施工队对广场进行围挡施工.如图,围挡经过直径的两端点A,B及圆周上两点C,D围成一个多边形ABPQR,其中AR,RQ,QP,PB分别与半圆相切于点A,D,C,B.已知该半圆半径OA长30米,∠COD为60°,设∠BOC为![]() .
.
(1)求围挡内部四边形OCQD的面积;
(2)为减少对市民出行的影响,围挡部分面积要尽可能小.求该围挡内部多边形ABPQR面积的最小值?并写出此时![]() 的值.
的值.
【答案】(1)![]() (2)围挡内部多边形ABPQR面积的最小值为900
(2)围挡内部多边形ABPQR面积的最小值为900![]() 平方米,此时
平方米,此时![]()
【解析】
(1)连接![]() 将四边形
将四边形![]() 变为两个全等的直角三角形,求得
变为两个全等的直角三角形,求得![]() 的长度后可计算得面积.(2)根据(1)的方法,求得多边形
的长度后可计算得面积.(2)根据(1)的方法,求得多边形![]() 的面积,求得总面积的表达式,利用换元法以及基本不等式求得多边形面积的最小值以及此时
的面积,求得总面积的表达式,利用换元法以及基本不等式求得多边形面积的最小值以及此时![]() 的值.
的值.
解:
(1)连接OQ,因为QD,QC为圆O的切线,所以QD=QC,OD=OC=30,
OQ=OQ,所以△ODQ≌△OCQ,所以∠DOQ=∠COQ=30°,
又因为OD⊥DQ,所以![]() =tan30°=
=tan30°=![]() ,所以DQ=10
,所以DQ=10![]() ,
,
所以S△ODQ=![]() OD·DQ=150
OD·DQ=150![]() ,所以SOCQD=2S△ODQ =300
,所以SOCQD=2S△ODQ =300![]() ;
;
即围挡内部四边形OCQD的面积为300![]() 平方米;
平方米;
(2)BP=OB tan![]() ,SOBPC=2S△OBP=900 tan
,SOBPC=2S△OBP=900 tan![]() ,同理SOARD=2S△OAR=900 tan(
,同理SOARD=2S△OAR=900 tan(![]() -
-![]() ),
),
SABPQR=900[tan![]() + tan(
+ tan(![]() -
-![]() )]+300
)]+300![]() ,
,![]()
即求 tan![]() + tan(
+ tan(![]() -
-![]() )的最小值,
)的最小值,
tan![]() + tan(
+ tan(![]() -
-![]() )= tan
)= tan![]() +
+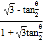 =
=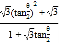 (*)
(*)
令![]() ,由
,由![]() 得x
得x![]() (1,4)
(1,4)
则(*)=![]() ≥
≥![]() ,当且仅当x=2时取等号,此时
,当且仅当x=2时取等号,此时![]() ,
,
故Smin=900×![]() +300
+300![]() =900
=900![]() ,
,
答:围挡内部多边形ABPQR面积的最小值为900![]() 平方米,此时
平方米,此时![]()


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员一次射击命中目标的概率分别是0.7,0.6,且每次射击命中与否相互之间没有影响,求:
(1)甲射击三次,第三次才命中目标的概率;
(2)甲、乙两人在第一次射击中至少有一人命中目标的概率;
(3)甲、乙各射击两次,甲比乙命中目标的次数恰好多一次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() .
.
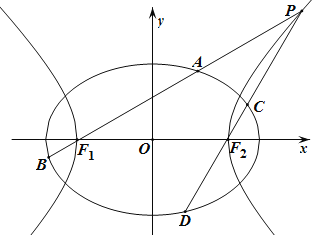
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() ;
;
(Ⅲ)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x、y轴分别交于点
与x、y轴分别交于点![]() 、
、![]() ,记以点
,记以点![]() 为圆心,半径为r的圆与三角形
为圆心,半径为r的圆与三角形![]() 的边的交点个数为M.对于下列说法:①当
的边的交点个数为M.对于下列说法:①当![]() 时,若
时,若![]() ,则
,则![]() ;②当
;②当![]() 时,若
时,若![]() ,则
,则![]() ;③当
;③当![]() 时,M不可能等于3;④M的值可以为0,1,2,3,4,5.其中正确的个数为( )
时,M不可能等于3;④M的值可以为0,1,2,3,4,5.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的体积为1.在侧棱
的体积为1.在侧棱![]() 上取一点
上取一点![]() ,使
,使![]() ,然后在
,然后在![]() 上取一点
上取一点![]() ,使
,使![]() ,继续在
,继续在![]() 上取一点
上取一点![]() ,使
,使![]() ,……按上述步骤,依次得到点
,……按上述步骤,依次得到点![]() ,记三棱锥
,记三棱锥![]() 的体积依次构成数列
的体积依次构成数列![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() .
.

(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,若不等式
项和,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过坐标原点的直线l与圆C:x2+y2﹣8x+12=0相交于不同的两点A,B.
(1)求线段AB的中点P的轨迹M的方程.
(2)是否存在实数k,使得直线l1:y=k(x﹣5)与曲线M有且仅有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有标号为![]() 的
的![]() 张标签,随机的选取两张标签.
张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业三月中旬生产![]() ,
,![]() ,
,![]() 三种产品共3000件,根据分层随机抽样的结果,企业统计员制作了如下的统计表格:
三种产品共3000件,根据分层随机抽样的结果,企业统计员制作了如下的统计表格:
产品类别 |
|
|
|
产品数量 | 1300 | ||
样本中的数量 | 130 |
由于不小心,表格中![]() ,
,![]() 产品的有关数据已被污染得看不清楚,统计员只记得样本中
产品的有关数据已被污染得看不清楚,统计员只记得样本中![]() 产品的数量比样本中
产品的数量比样本中![]() 产品的数量多10.根据以上信息,求该企业生产
产品的数量多10.根据以上信息,求该企业生产![]() 产品的数量.
产品的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com