[题目]一个盒子里装有标号为的张标签.随机的选取两张标签.(1)若标签的选取是无放回的.求两张标签上的数字为相邻整数的概率,(2)若标签的选取是有放回的.求两张标签上的数字至少有一个为5的概率. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】一个盒子里装有标号为的张标签，随机的选取两张标签.

（1）若标签的选取是无放回的，求两张标签上的数字为相邻整数的概率；

（2）若标签的选取是有放回的，求两张标签上的数字至少有一个为5的概率.

【答案】（1）（2）

【解析】

（1）先求出无放回的从5张标签随机地选取两张标签的基本事件总数，再求出两张标签上的数字为相邻整数的基本事件数，从而得到概率；

（2）先求出有放回的从5张标签随机地选取两张标签的基本事件总数，再求出两张标签上的数字至少有一个为5的基本事件数，从而得到概率.

解：（1）由题意知本题是一个等可能事件的概率，无放回的从5张标签随机地选取两张标签的基本事件有个，
两张标签上的数字为相邻整数基本事件有个，
∴根据等可能事件的概率公式得到；

（2）由题意知本题是一个等可能事件的概率，有放无回的从5张标签随机地选取两张标签的基本事件有个，

两张标签上的数字至少有一个为5的基本事件有个，

∴根据等可能事件的概率公式得到.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）.为了探究车流量与的浓度是否有关，现采集到某城市周一至周五某一时间段车流量与的浓度的数据如下表：

时间	周一	周二	周三	周四	周五
车流量（万辆）	100	102	108	114	116
的浓度（微克/立方米）	78	80	84	88	90

（1）根据上表数据，用最小二乘法求出关于的线性回归方程；

（2）若周六同一时间段车流量是200万辆，试根据（1）求出的线性回归方程，预测此时的浓度为多少.

参考公式：,.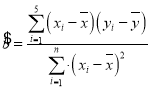

查看答案和解析>>

科目：高中数学 来源： 题型：

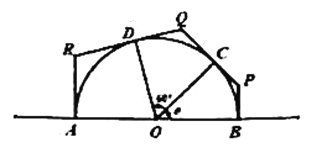
【题目】为美化城市环境，相关部门需对一半圆形中心广场进行改造出新，为保障市民安全，施工队对广场进行围挡施工．如图，围挡经过直径的两端点A，B及圆周上两点C，D围成一个多边形ABPQR，其中AR，RQ，QP，PB分别与半圆相切于点A，D，C，B．已知该半圆半径OA长30米，∠COD为60°，设∠BOC为．

（1）求围挡内部四边形OCQD的面积；

（2）为减少对市民出行的影响，围挡部分面积要尽可能小．求该围挡内部多边形ABPQR面积的最小值？并写出此时的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（用数字作答）从5本不同的故事书和4本不同的数学书中选出4本，送给4位同学，每人1本，问：

（1）如果故事书和数学书各选2本，共有多少种不同的送法？

（2）如果故事书甲和数学书乙必须送出，共有多少种不同的送法？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图1为某省2018年1~4月快递业务量统计图，图2是该省2018年1~4月快递业务收入统计图，下列对统计图理解错误的是（）

A. 2018年1~4月的业务量，3月最高，2月最低，差值接近2000万件

B. 2018年1~4月的业务量同比增长率均超过50%，在3月底最高

C. 从两图来看，2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致

D. 从1~4月来看，该省在2018年快递业务收入同比增长率逐月增长

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】近年来，来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”：高铁、扫码支付、共享单车和网购．其中共享单车既响应绿色出行号召，节能减排，保护环境，又方便人们短距离出行，增强灵活性．某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车，三种车的计费标准均为每15分钟（不足15分钟按15分钟计）1元，按每日累计时长结算费用，例如某人某日共使用了24分钟，系统计时为30分钟．A同学统计了他1个月（按30天计）每天使用共享单车的时长如茎叶图所示，不考虑每月自然因素和社会因素的影响，用频率近似代替概率．设A同学每天消费元．

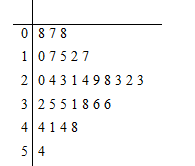
（1）求的分布列及数学期望；

（2）各品牌为推广用户使用，推出APP注册会员的优惠活动：红车月功能使用费8元，每天消费打5折；黄车月功能使用费20元，每天前15分钟免费，之后消费打8折；蓝车月功能使用费45元，每月使用22小时之内免费，超出部分按每15分钟1元计费．设分别为红车，黄车，蓝车的月消费，写出与的函数关系式，参考（1）的结果，A同学下个月选择其中一个注册会员，他选哪个费用最低？