
【题目】近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费![]() 元.
元.
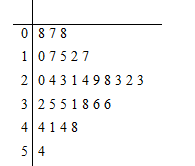
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设![]() 分别为红车,黄车,蓝车的月消费,写出
分别为红车,黄车,蓝车的月消费,写出![]() 与
与![]() 的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌的共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 | (0,15] | (15,30] | (30,45] | (45,60] |
人数 | 16 | 45 | 34 | 5 |
在(2)的活动条件下,每个品牌各应该投放多少辆?
【答案】(1)分布列见解析,![]() (2)选红车(3)480,1500,1020
(2)选红车(3)480,1500,1020
【解析】
(1)根据茎叶图![]() 可能的取值有
可能的取值有![]() ,分别求出其分布列及期望即可;
,分别求出其分布列及期望即可;
(2)根据题意分别写出![]() 与
与![]() 的函数关系式,并算出A同学在每种优惠活动下的费用,看哪个费用最低即可;
的函数关系式,并算出A同学在每种优惠活动下的费用,看哪个费用最低即可;
(3)算出每个时长下每个品牌的费用,比较大小,确定每个时长下选择的最优惠的品牌,根据比例算出每个品牌各应该投放的辆数.
解:(1)根据茎叶图统计A同学30天里面每天使用共享单车的时长![]() 有6天,
有6天,![]() 有12天,
有12天,![]() 有10天,
有10天,![]() 有2天,
有2天,
则![]() 可能的取值有
可能的取值有![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 1 | 2 | 3 | 4 |
|
|
|
|
|
![]() ;
;
(2)红车![]() ,即
,即![]() ;
;
黄车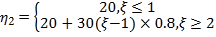 ,即
,即![]() ;
;
蓝车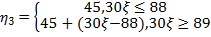 ,即
,即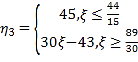 ;
;
若A同学下个月选择红车注册会员,则其消费为:![]() 元,
元,
若A同学下个月选择黄车注册会员,则其消费为:![]() 元,
元,
若A同学下个月选择蓝车注册会员,则其消费为:![]() 元,
元,
故选红车费用最低;
(3)当平均时长为(0,15]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选黄车;
元,故此时选黄车;
当平均时长为(15,30]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选红车;
元,故此时选红车;
当平均时长为(30,45]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选蓝车;
元,故此时选蓝车;
当时长为(45,60]时,红车消费![]() 元,黄车消费
元,黄车消费![]() 元,蓝车消费
元,蓝车消费![]() 元,故此时选红车;
元,故此时选红车;
故选红车的人数为50,选黄车的人数为16,选蓝车的人数为34,
故红车应该投放![]() 辆,黄车应该投放
辆,黄车应该投放![]() 辆,蓝车应该投放
辆,蓝车应该投放![]() 辆,
辆,
综合:红车应该投放![]() 辆,黄车应该投放
辆,黄车应该投放![]() 辆,蓝车应该投放
辆,蓝车应该投放![]() 辆.
辆.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() ,其中
,其中![]() ,
,![]() 为实数,事件
为实数,事件![]() 为“函数
为“函数![]() 在区间
在区间![]() 为增函数”.
为增函数”.
(1)若![]() 为区间
为区间![]() 上的整数值随机数,
上的整数值随机数,![]() 为区间
为区间![]() 上的整数值随机数,求事件
上的整数值随机数,求事件![]() 发生的概率;
发生的概率;
(2)若![]() 为区间
为区间![]() 上的均匀随机数,
上的均匀随机数,![]() 为区间
为区间![]() 上的均匀随机数,求事件
上的均匀随机数,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的体积为1.在侧棱
的体积为1.在侧棱![]() 上取一点
上取一点![]() ,使
,使![]() ,然后在
,然后在![]() 上取一点
上取一点![]() ,使
,使![]() ,继续在
,继续在![]() 上取一点
上取一点![]() ,使
,使![]() ,……按上述步骤,依次得到点
,……按上述步骤,依次得到点![]() ,记三棱锥
,记三棱锥![]() 的体积依次构成数列
的体积依次构成数列![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() .
.

(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,若不等式
项和,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年国庆黄金周旅游市场依旧火爆.一旅行社为某旅行团包机旅游,其中旅行社的包机费15000元,旅行团中每人的飞机票按以下方式与旅行社结算:若旅行团人数不超过35人,飞机票每张800元;若旅行团人数多于35人,则给予如下优惠:每多1人,每张机票减少10元,但旅行团的人数最多不超过60人,记旅行团人数为![]() ,每个人的机票钱为y元.
,每个人的机票钱为y元.
(1)写出![]() 与
与![]() 的关系式.
的关系式.
(2)求旅行社获得的利润![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有标号为![]() 的
的![]() 张标签,随机的选取两张标签.
张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R.若存在与x无关的正常数M,使|f(x)|≤ M|x|对一切实数x均成立,则称f(x)为有界泛函.则函数:① f(x)=-3x,② f(x)=x2,③ f(x)=sin2x,④ f(x)=2x,⑤ f(x)=xcosx中,属于有界泛函的有____________.(填上所有正确的番号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() .
.
(1)若a=4,求函数f(x)的单调区间;
(2)若函数f(x)在区间(0,1]内单调递增,求实数a的取值范围;
(3)若x1、x2∈R+,且x1≤x2,求证:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(附:![]() ,
,![]() ,
,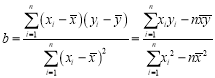 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本平均值)
为样本平均值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com