练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    “三角形有一个内角为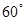”是“三内角成等差数列”的（     ）

    A．充分不必要条件                        B．必要不充分条件

    C．充要条件                             D．既不充分也不必要条件

     

    【答案】

    C

    【解析】

    试题分析：根据题意，当条件成立时，则可知该角不是最大角时毕竟为等边三角形，如果该角是最小角，三角形也是等边三角形，满足题，当该角不是最大角和最小角时，毕竟满足内角和定理，另外两个角的和为120度，构成了等差数列。反之也成立，故是充要条件。选C.

    考点：等差数列

    点评：本试题考查了充分条件以及等差数列的概念的运用，属于基础题。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2005•上海模拟）（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
    （2）若三角形有一个内角为arccos
    7
    9
    ，周长为定值p，求面积S的最大值；
    （3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
    1
    2
    absinC≤
    1
    2
    ×9×8sinC=36sinC    ，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时cosC=
    43
    48
    ，sinC=
    		455
    48
    ，所以，该三角形面积的最大值是
    3
    		455
    4
    ．以上解答是否正确？若不正确，请你给出正确的解答．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•上海模拟）（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
    （2）若三角形有一个内角为arccos
    79
    ，周长为定值p，求面积S的最大值；
    （3）为了研究边长a，b，c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）=[（a+b）2-c2][c2-（a-b）2]=-c4+2（a2+b2）c2-（a2-b2）2=-[c2-（a2+b2）]2+4a2b2
    而-[c2-（a2+b2）]2≤0，a2≤81，b2≤64，则S≤36，但是，其中等号成立的条件是c2=a2+b2，a=9，b=8，于是c2=145与3≤c≤4矛盾，所以，此三角形的面积不存在最大值．
    以上解答是否正确？若不正确，请你给出正确的答案．
    （注：16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）称为三角形面积的海伦公式，它已经被证明是正确的）

    查看答案和解析>>

    科目：高中数学 来源：上海模拟 题型：解答题

    （1）若直角三角形两直角边长之和为12，求其周长p的最小值；
    （2）若三角形有一个内角为arccos
    7
    9
    ，周长为定值p，求面积S的最大值；
    （3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
    1
    2
    absinC≤
    1
    2
    ×9×8sinC=36sinC    ，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时cosC=
    43
    48
    ，sinC=
    		455
    48
    ，所以，该三角形面积的最大值是
    3
    		455
    4
    ．以上解答是否正确？若不正确，请你给出正确的解答．

    查看答案和解析>>

    科目：高中数学 来源：2004-2005学年上海市十校高三联考数学试卷（文科）（解析版） 题型：解答题

    （1）若直角三角形两直角边长之和为12，求其周长p的最小值；
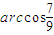    （2）若三角形有一个内角为，周长为定值p，求面积S的最大值；
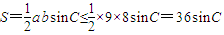    （3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时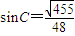，，所以，该三角形面积的最大值是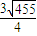．以上解答是否正确？若不正确，请你给出正确的解答．

    查看答案和解析>>

    同步练习册答案