
分析 利用平面向量的线性表示和数量积,结合勾股定理,即可证明结论成立.
解答 证明:Rt△CAB中,AD是斜边BC上的中线,如图所示;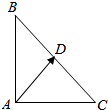
∴$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴${\overrightarrow{AD}}^{2}$=$\frac{1}{4}$(${\overrightarrow{AB}}^{2}$+2$\overrightarrow{AB}$•$\overrightarrow{AC}$+${\overrightarrow{AC}}^{2}$)=$\frac{1}{4}$(${\overrightarrow{AB}}^{2}$+${\overrightarrow{AC}}^{2}$),
∴|$\overrightarrow{AD}$|=$\frac{1}{2}$$\sqrt{{\overrightarrow{|AB|}}^{2}{+\overrightarrow{|AC|}}^{2}}$
${\overrightarrow{|AB|}}^{2}$+${\overrightarrow{|AC|}}^{2}$=${\overrightarrow{|BC|}}^{2}$
∴|$\overrightarrow{AD}$|=$\frac{1}{2}$|$\overrightarrow{BC}$|.
点评 本题考查了平面向量的应用问题,也考查了勾股定理的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?
如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
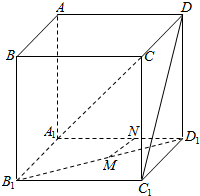 在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.
在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N?Q?Z?R | B. | N?Z?Q?R | C. | R?Q?Z?N | D. | Z?N?Q?R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com