Question

【题目】已知函数f(x)＝－x2－2x，g(x)＝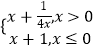
（1）求g[f(1)]的值；
（2）若方程g[f(x)]－a＝0有4个实数根，求实数a的取值范围．

Answer 1

【答案】
（1）解：利用解析式直接求解得g[f(1)]＝g(－3)＝－3＋1＝－2.
（2）解：令f(x)＝t，则原方程化为g(t)＝a，易知方程f(x)＝t在t∈(－∞，1)内有2个不同的解，则原方程有4个解等价于函数y＝g(t)(t<1)与y＝a的图象有2个不同的交点，作出函数y＝g(t)(t<1)的图象，由图象可知，当1≤a< 时，函数y＝g(t)(t<1)与y＝a有2个不同的交点，即所求a的取值范围是 .
【解析】由题意可得函数y=g[f（x）]与函数y=a有4个交点，结合图象可得实数a的取值范围．根的存在问题相对来说是零点里头最重要的一个点，也是比较常考的点，一般都是以中档题的形式在选择题里出现，在解这种题的时候，做出函数图象是首要选择，然后根据图形去寻找答案．