
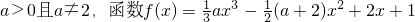 .
.解:(1)∵f(x)=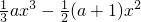 +2x+1
+2x+1
∴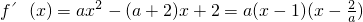 …(2分)a>2时,列表如下,
…(2分)a>2时,列表如下,
| x | 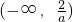 |  | 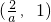 | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
∴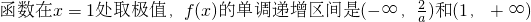
单调递减区间是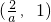
当0<a<2时,列表如下,
| x | (-∞,1) | 1 | 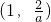 |  | 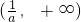 |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
∴
单调递减区间是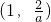
(2)因为f(0)=1,由(1)知要使在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,只需在区间(0,+∞)上f(x)极小值<1即可.
当a>2时,f(x)极小值=f(1)=2- <1,所以a>6.
<1,所以a>6.
当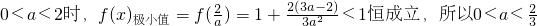 .
.
综上所述,实数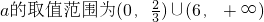


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
| a |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2007年甘肃省天水一中高考数学三模试卷(文科)(解析版) 题型:解答题
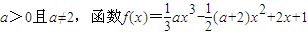 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com