
【题目】折纸是一项艺术,可以折出很多数学图形.将一张圆形纸片放在平面直角坐标系中,圆心B(-1,0),半径为4,圆内一点A为抛物线![]() 的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点
的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点![]() 始终与点A重合,将纸展平,得到一条折痕,设折痕与线段
始终与点A重合,将纸展平,得到一条折痕,设折痕与线段![]() B的交点为P.
B的交点为P.
(Ⅰ)将纸片展平后,求点P的轨迹C的方程;
(Ⅱ)已知过点A的直线l与轨迹C交于R,S两点,当l无论如何变动,在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点,求点T的坐标.
所在直线一定经过原点,求点T的坐标.
【答案】(Ⅰ)轨迹C的方程为![]() ;(Ⅱ)点T的坐标为(4,0).
;(Ⅱ)点T的坐标为(4,0).
【解析】
(Ⅰ)依题意知PA=P![]() ,P的轨迹是以B、A为焦点,长轴长为4,焦距为2的椭圆,由题意能求出其椭圆方程;(Ⅱ)题意等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称,当直线l垂直于x轴时,x轴上任意一点都满足TS与TR所在直线关于x轴对称,当直线l不垂直于x轴时,假设存在T(t,0)满足条件,设l的方程为y=k(x﹣1),R(x1,y1),S(x2,y2),联立
,P的轨迹是以B、A为焦点,长轴长为4,焦距为2的椭圆,由题意能求出其椭圆方程;(Ⅱ)题意等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称,当直线l垂直于x轴时,x轴上任意一点都满足TS与TR所在直线关于x轴对称,当直线l不垂直于x轴时,假设存在T(t,0)满足条件,设l的方程为y=k(x﹣1),R(x1,y1),S(x2,y2),联立![]() ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根与系数的关系、根的判别式、直线关于x轴对称,结合已知条件能求出存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称.
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根与系数的关系、根的判别式、直线关于x轴对称,结合已知条件能求出存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称.
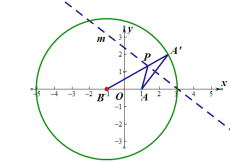
(Ⅰ)依题意:折痕所在直线m为线段![]() 的垂直平分线,∴PA=P
的垂直平分线,∴PA=P![]() ,
,
∴PB+PA= PB + P![]() =4>2,
=4>2,
∴P的轨迹是以B、A为焦点,长轴长为4,焦距为2的椭圆.
∴b2=3.
∴椭圆方程为![]() .
.
(Ⅱ)由题意可知:在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称
所在直线一定经过原点等价于在AB所在直线上存在一点T,使得TS与TR所在直线关于x轴对称
当直线l垂直于x轴时,x轴上任意一点都满足TS与TR所在直线关于x轴对称,
当直线l不垂直于x轴时,假设存在T(t,0)满足条件,
设l的方程为y=k(x﹣1),R(x1,y1),S(x2,y2),
联立![]() ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,
由根与系数的关系得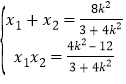 ,①,其中△>0,
,①,其中△>0,
∵TS与TR所在直线关于x轴对称,∴![]() =0,②
=0,②
∵R,S两点在直线y=k(x﹣1)上,
∴y1=k(x1﹣1),y2=k(x2﹣1),代入②,得:
![]() =
=![]() =0,
=0,
∴2x1x2﹣(t+1)(x1+x2)+2t=0,③
将①代入③,得![]() =
=![]() =0,④
=0,④
要使得④与k的取值无关,则t=4,
综上所述,存在T(4,0),使得当l变化时,总有TS与TR所在直线关于x轴对称,即在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点.
所在直线一定经过原点.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 两点的动点,求
两点的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,且以线段
,且以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,椭圆
相切,椭圆![]() 截直线
截直线![]() 所得线段的长度为1.
所得线段的长度为1.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了改善市民的生活环境,长沙某大型工业城市决定对长沙市的1万家中小型化工企业进行污染情况摸排,并出台相应的整治措施.通过对这些企业的排污口水质,周边空气质量等的检验,把污染情况综合折算成标准分100分,发现长沙市的这些化工企业污染情况标准分基本服从正态分布N(50,162),分值越低,说明污染越严重;如果分值在[50,60]内,可以认为该企业治污水平基本达标.
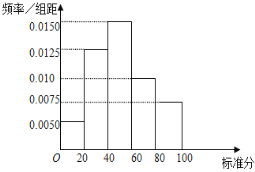
(Ⅰ)如图为长沙市的某工业区所有被调査的化工企业的污染情况标准分的频率分布直方图,请计算这个工业区被调査的化工企业的污染情况标准分的平均值,并判断该工业区的化工企业的治污平均值水平是否基本达标;
(Ⅱ)大量调査表明,如果污染企业继续生产,那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元,标准分在[18,34)内的化工企业每月对周边造成的直接损失约为4万元.长沙市决定关停80%的标准分低于18分的化工企业和60%的标准分在[18,34)内的化工企业,每月可减少的直接损失约有多少?
(附:若随机变量![]() ,则
,则![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
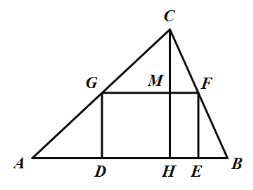
【题目】某市有一面积为12000平方米的三角形地块![]() ,其中边
,其中边![]() 长为200米,现计划建一个如图所示的长方形停车场
长为200米,现计划建一个如图所示的长方形停车场![]() ,停车场的四个顶点都在
,停车场的四个顶点都在![]() 的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设
的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设![]() 米,建设工程的总费用为
米,建设工程的总费用为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数表达式:
的函数表达式:
(2)求停车场面积最大时![]() 的值,并求此时的工程总费用.
的值,并求此时的工程总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com