
若等差数列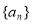 和等比数列
和等比数列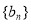 的首项均为1,且公差
的首项均为1,且公差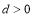 ,公比
,公比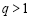 ,则集合
,则集合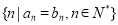 的元素个数最多有 个.
的元素个数最多有 个.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷理科数学试卷(解析版) 题型:解答题
在平面直角坐标系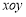 中,已知椭圆的焦点在
中,已知椭圆的焦点在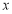 轴上,离心率为
轴上,离心率为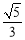 ,且经过点
,且经过点 .
.
(1)求椭圆的标准方程;
(2) 以椭圆的长轴为直径作圆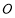 ,设
,设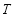 为圆
为圆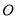 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点,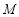 为
为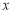 轴上一点,过圆心
轴上一点,过圆心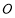 作直线
作直线 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点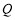 .问:直线
.问:直线 能否与圆
能否与圆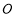 总相切,如果能,求出点
总相切,如果能,求出点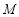 的坐标;如果不能,说明理由.
的坐标;如果不能,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二理科数学试卷(解析版) 题型:解答题
据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为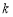
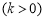 .现已知相距18
.现已知相距18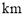 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为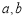 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数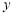 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设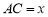 (
(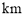 ).
).
(1)试将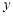 表示为
表示为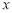 的函数; (2)若
的函数; (2)若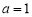 ,且
,且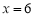 时,
时,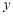 取得最小值,试求
取得最小值,试求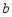 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:解答题
如果函数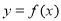 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意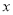 ,存在实数
,存在实数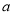 使得
使得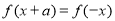 成立,则称此函数具有“
成立,则称此函数具有“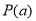 性质”。
性质”。
(1)判断函数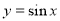 是否具有“
是否具有“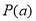 性质”,若具有“
性质”,若具有“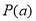 性质”,求出所有
性质”,求出所有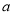 的值;若不具有“
的值;若不具有“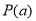 性质”,说明理由;
性质”,说明理由;
(2)已知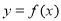 具有“
具有“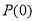 性质”,且当
性质”,且当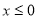 时
时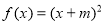 ,求
,求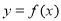 在
在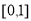 上有最大值;
上有最大值;
(3)设函数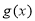 具有“
具有“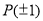 性质”,且当
性质”,且当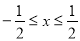 时,
时,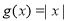 .若
.若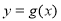 与
与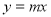 交点个数为2013,求
交点个数为2013,求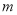 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:填空题
若关于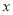 的不等式
的不等式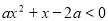 的解集中有且仅有4个整数解,则实数
的解集中有且仅有4个整数解,则实数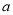 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:填空题
某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种,从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测三数学试卷(解析版) 题型:解答题
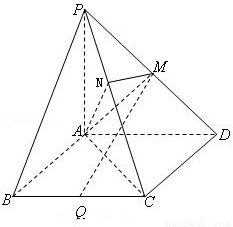
如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是平行四边形,且AC⊥CD,PA=AD,M,Q分别是PD,BC的中点.
(1)求证:MQ∥平面PAB;
(2)若AN⊥PC,垂足为N,求证:MN⊥PD.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练理科数学试卷(解析版) 题型:解答题
如图所示的几何体中,面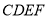 为正方形,面
为正方形,面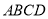 为等腰梯形,
为等腰梯形, 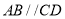 ,
,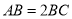 ,
,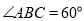 ,且平面
,且平面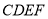
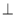 平面
平面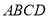 .
.
(1)求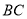 与平面
与平面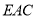 所成角的正弦值;
所成角的正弦值;
(2)线段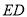 上是否存在点
上是否存在点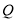 ,使平面
,使平面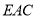
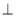 平面
平面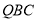 ?
?
证明你的结论.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:解答题
在数列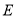 中,已知
中,已知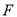 ,
,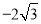 ,
,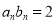 (
(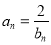 ,
,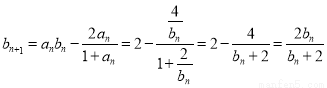 ).
).
(1)当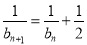 ,
,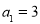 时,分别求
时,分别求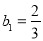 的值,判断
的值,判断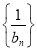 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数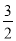 ,使得
,使得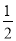 为完全平方数.
为完全平方数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com