
某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种,从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二理科数学试卷(解析版) 题型:填空题
设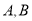 分别是椭圆
分别是椭圆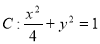 的上下两个顶点,
的上下两个顶点,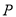 为椭圆
为椭圆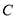 上任意一点(不与点
上任意一点(不与点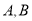 重合),直线
重合),直线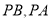 分别交
分别交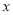 轴于
轴于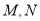 两点,若椭圆
两点,若椭圆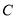 在
在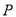 点的切线交
点的切线交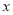 轴于
轴于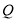 点,则
点,则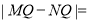 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:解答题
在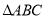 中,角
中,角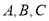 所对的边分别为
所对的边分别为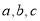 。已知
。已知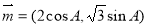 ,
,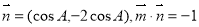 .
.
(1)若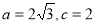 ,求
,求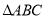 的面积; (2)求
的面积; (2)求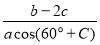 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:填空题
若等差数列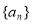 和等比数列
和等比数列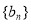 的首项均为1,且公差
的首项均为1,且公差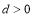 ,公比
,公比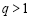 ,则集合
,则集合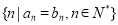 的元素个数最多有 个.
的元素个数最多有 个.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测三数学试卷(解析版) 题型:解答题
已知椭圆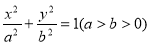 的左右焦点分别为
的左右焦点分别为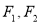 ,短轴两个端点为
,短轴两个端点为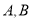 ,且四边形
,且四边形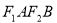 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若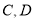 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点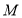 满足
满足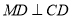 ,连接
,连接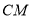 ,交椭圆于点
,交椭圆于点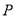 .证明:
.证明: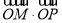 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点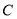 的定点
的定点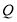 ,使得以
,使得以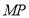 为直径的圆恒过直线
为直径的圆恒过直线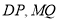 的交点,若存在,求出点
的交点,若存在,求出点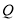 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练理科数学试卷(解析版) 题型:解答题
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点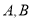 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:解答题
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC, DE交AB于点F.求证:△PDF∽△POC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com