
各项均为正数的数列{an}满足an2=4Sn-2an-1(n∈N*),其中Sn为{an}的前n项和.
(1)求a1,a2的值;
(2)求数列{an}的通项公式;
(3)是否存在正整数m、n,使得向量a=(2an+2,m)与向量b=(-an+5,3+an)垂直?说明理由.
(1) a1=1 a2=3 (2) an=2n-1 (3)见解析
【解析】解:(1)当n=1时,
A12=4S1-2a1-1=2a2-1,
即(a1-1)2=0,解得a1=1.
当n=2时,a22=4S2-2a2-1=4a1+2a2-1=3+2a2,
解得a2=3或a2=-1(舍去).
(2)an2=4Sn-2an-1,①
An+12=4Sn+1-2an+1-1.②
②-①得:a n+12-an2=4an+1-2an+1+2an
=2(an+1+an),
即(an+1-an)(an+1+an)=2(an+1+an).
∵数列{an}各项均为正数,
∴an+1+an>0,an+1-an=2,
∴数列{an}是首项为1,公差为2的等差数列.
∴an=2n-1.
(3)∵an=2n-1,
∴a=(2an+2,m)=(2(2n+3),m)≠0,b=(-an+5,3+an)=(-(2n+9),2(n+1))≠0,
∴a⊥b⇔a·b=0
⇔m(n+1)=(2n+3)(2n+9)=[2(n+1)+1][2(n+1)+7]
⇔m(n+1)=4(n+1)2+16(n+1)+7
⇔m=4(n+1)+16+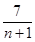 .
.
∵m,n∈N*,
∴n+1=7,m=4×7+16+1,
即n=6,m=45.
∴当n=6,m=45时,a⊥b.


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | 2 n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| bn |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| bn+1 |
| bn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com