
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() 在
在![]() 上存在两个极值点,求
上存在两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() ,
,![]() ,函数
,函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 线段的中点为
线段的中点为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;;(2)见解析.
;;(2)见解析.
【解析】
(1)求导,依题意,导函数满足![]() 在
在![]() 上有两个不等实根,转化可得
上有两个不等实根,转化可得![]() ,构造函数
,构造函数![]() ,利用导数可知
,利用导数可知![]() ,且由
,且由![]() 的趋近性可求得实数
的趋近性可求得实数![]() 的取值范围;
的取值范围;
(2)问题转化为证明![]() ,通过换元令
,通过换元令![]() ,即证
,即证![]() ,再分别证明即可.
,再分别证明即可.
(1)由题意可知,![]() ,令
,令![]() ,
,
则![]() 在
在![]() 上存在两个极值点等价于
上存在两个极值点等价于![]() 在
在![]() 上有两个不等实根,
上有两个不等实根,
由![]() 可得
可得![]() ,
,
令![]() ,则
,则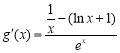 ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() 是
是![]() 的极大值也是最大值,
的极大值也是最大值,
![]()
![]() ,
,
![]()
![]() ,
,
又当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 大于0且趋向于0,
大于0且趋向于0,
要使![]() 在
在![]() 有两个根,则
有两个根,则![]() ;
;
(2)由题意可得![]() ,
,![]() ,
,
要证![]() (1)
(1)![]() 成立,
成立,
只需证![]() ,即
,即![]() ,
,
设![]() ,即证
,即证![]() ,
,
要证![]() ,只需证
,只需证![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,即
,即![]() 成立;
成立;
要证![]() ,只需证
,只需证![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上为减函数,
上为减函数,
![]() ,即
,即![]() 成立;
成立;
![]()
![]() 成立,
成立,
即![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】2020年3月12日,国务院新闻办公室发布会重点介绍了改革开放40年,特别是党的十八大以来我国脱贫攻坚、精准扶贫取得的显著成绩,这些成绩为全面脱贫初步建成小康社会奠定了坚实的基础.下图是统计局公布的2010年~2019年年底的贫困人口和贫困发生率统计表.则下面结论正确的是( )
(年底贫困人口的线性回归方程为![]() (其中
(其中![]() 年份-2019),贫困发生率的线性回归方程为
年份-2019),贫困发生率的线性回归方程为![]() (其中
(其中![]() 年份-2009))
年份-2009))

A.2010年~2019年十年间脱贫人口逐年减少,贫困发生率逐年下降
B.2012年~2019年连续八年每年减贫超过1000万,且2019年贫困发生率最低
C.2010年~2019年十年间超过1.65亿人脱贫,其中2015年贫困发生率低于6%
D.根据图中趋势线可以预测,到2020年底我国将实现全面脱贫
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,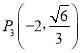 ,
,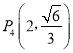 中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
(1)求椭圆C的方程;
(2)过左焦点F1且不平行坐标轴的直线l交椭圆于P、Q两点,若PQ的中点为N,O为原点,直线ON交直线x=﹣3于点M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国数学家庞加是个喜欢吃面包的人,他每天都会购买一个面包,面包师声称自己出售的每个面包的平均质量是1000![]() ,上下浮动不超过50
,上下浮动不超过50![]() .这句话用数学语言来表达就是:每个面包的质量服从期望为1000
.这句话用数学语言来表达就是:每个面包的质量服从期望为1000![]() ,标准差为50
,标准差为50![]() 的正态分布.
的正态分布.
(1)假设面包师的说法是真实的,从面包师出售的面包中任取两个,记取出的两个面包中质量大于1000![]() 的个数为
的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)作为一个善于思考的数学家,庞加莱每天都会将买来的面包称重并记录,25天后,得到数据如下表,经计算25个面包总质量为24468![]() .庞加莱购买的25个面包质量的统计数据(单位:
.庞加莱购买的25个面包质量的统计数据(单位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
尽管上述数据都落在![]() 上,但庞加菜还是认为面包师撒谎,根据所附信息,从概率角度说明理由
上,但庞加菜还是认为面包师撒谎,根据所附信息,从概率角度说明理由
附:
①若![]() ,从X的取值中随机抽取25个数据,记这25个数据的平均值为Y,则由统计学知识可知:随机变量
,从X的取值中随机抽取25个数据,记这25个数据的平均值为Y,则由统计学知识可知:随机变量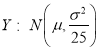
②若![]() ,则
,则![]() ,
,![]() ,
,![]() ;
;
③通常把发生概率在0.05以下的事件称为小概率事件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为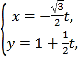 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com