
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 处取得极值,对
处取得极值,对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ①当![]() 时,
时,![]() 的递减区间是
的递减区间是![]() ,无递增区间;②当
,无递增区间;②当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() .
.
(2) ![]() .
.
【解析】分析:(1)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由函数
的减区间;(2)由函数![]() 在
在![]() 处取得极值,可得
处取得极值,可得![]() ,
,![]() ,等价于
,等价于![]()
利用导数研究函数的单调性可得以![]() ,从而得
,从而得![]() .
.
详解:(1)在区间上![]() ,
,![]()
①若![]() ,则
,则![]() ,
,![]() 是区间
是区间![]() 上的减函数;
上的减函数;
②若![]() ,令
,令![]() 得
得![]()
在区间![]() 上,
上,![]() ,函数
,函数![]() 是减函数;
是减函数;
在区间![]() 上,
上,![]() ,函数
,函数![]() 是增函数;
是增函数;
综上所述,①当![]() 时,
时,![]() 的递减区间是
的递减区间是![]() ,无递增区间;
,无递增区间;
②当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() .
.
(2)因为函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]()
解得![]() ,经检验满足题意.
,经检验满足题意.
由已知![]() ,则
,则![]()
令![]() ,则
,则![]()
易得![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ,即
,即![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 证明:Tn+12=﹣2an+10bn(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为 ![]() 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为 ![]() ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.

(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设10≤x1<x2<x3<x4≤104 , x5=105 , 随机变量ξ1取值x1、x2、x3、x4、x5的概率均为0.2,随机变量ξ2取值 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
A.Dξ1>Dξ2
B.Dξ1=Dξ2
C.Dξ1<Dξ2
D.Dξ1与Dξ2的大小关系与x1、x2、x3、x4的取值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )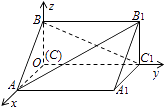
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)设![]() ,若函数
,若函数![]() 的图象的一条对称轴为直线
的图象的一条对称轴为直线![]() ,求
,求![]() 的值;
的值;
(2)若将![]() 的图象向左平移
的图象向左平移![]() 个单位,或者向右平移
个单位,或者向右平移![]() 个单位得到的图象都过坐标原点,求所有满足条件的
个单位得到的图象都过坐标原点,求所有满足条件的![]() 和
和![]() 的值;
的值;
(3)设![]() ,
,![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的所有零点依次为
上的所有零点依次为![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com